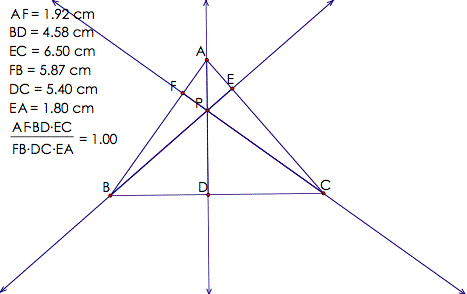
Ceva’s Theorem

By Mary Negley

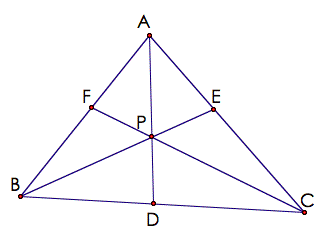
For this write-up, I will explore Ceva’s Theorem, which states that given a triangle, the three lines,, and intersect at point iff . A GSP sketch is given below.

An interesting fact about point P is that it may be anywhere on the plane. I will look at P in the following cases: (1) when P is the centroid, (2) when P is the orthocenter, (3) when P is the incenter, and (4) when P is the circumcenter.

Case1: P is the centroid. By definition of centroid, P is the intersection of the medians of the triangle. Below is a GSP sketch of this case.

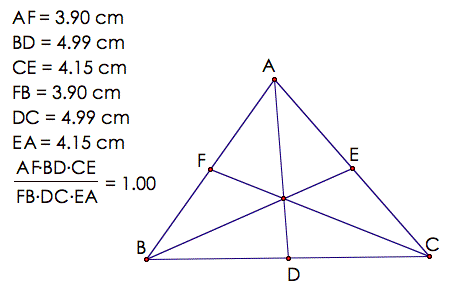
Clearly, the ratio holds in this case.

Case2: P is the orthocenter. By definition of orthocenter, P is the intersection of the lines of the altitudes of the triangle. Below is a GSP sketch of this case.

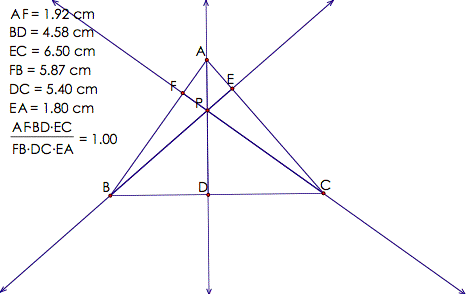
Clearly, the ratio holds in this case.

Case3: P is the incenter. By definition of incenter, P is the intersection of the angle bisectors of the triangle. Below is a GSP sketch of this case.

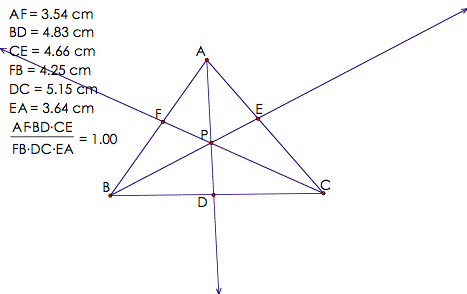
Clearly, the ratio holds in this case.

Case4: P is the circumcenter. By definition of circumcenter, P is the intersection of the perpendicular bisectors of the sides of the triangle. Below is a GSP sketch of this case.

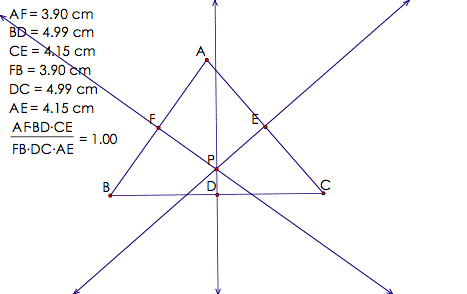
Clearly, the ratio holds in this case.

Proof: Now I will show that given a triangle, the three lines,, and intersect at point iff .

First I will assume that the three lines intersect at point P and then I will show that.

Below is the triangle.

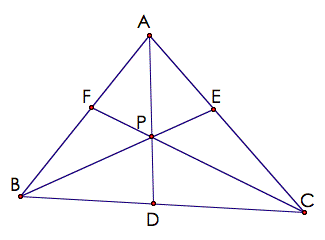
To aid me in my proof, I will extend the segments AD, BE, and CF to be lines and I will draw a line through C, which is parallel to AB. Below is the new sketch.

Now I will shade in a couple of the similar triangles that occur.

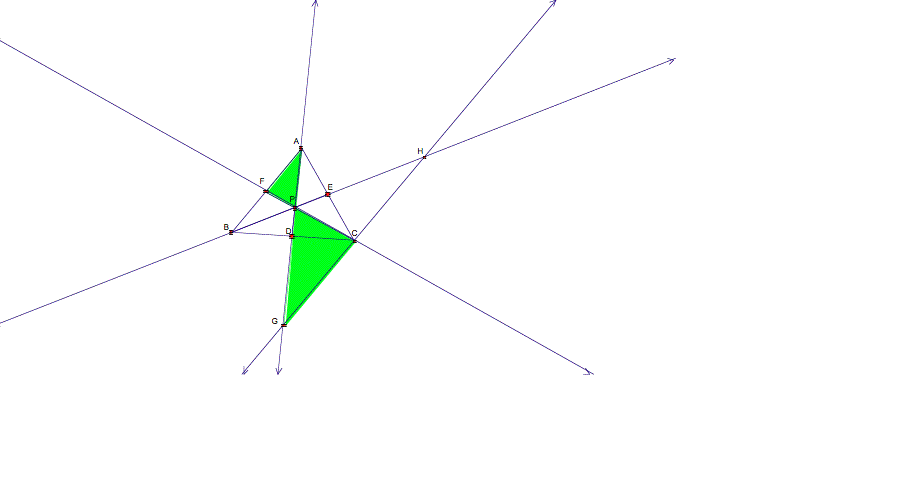
Triangle GCP ~ Triangle AFP because

1) by congruency of alternate interior angles

2) by congruency of vertical angle theorem

and 3) since and ,

and by 1) and 2)

so subtracting <PGC and <CPG from both sides yields .

Similarly, Triangle GCD ~ Triangle ABD, Triangle HCP ~ Triangle BFP and Triangle HEC ~ Triangle BEA,

Since the preceding triangles are similar, the following ratios occur:

(1)

(2)

(3)

(4)

To show that, I can show that.

By using (1), (3) and the property of transitivity, I get that . Solving for HC, I get . Solving for HC in (4) yields . By transitivity, . Now I will cross-multiply and get . Then, solving for GC in (2) yields and when I substitute that into my equality, I get . By simplifying and cross-multiplying, I get . Hence, .

Thus far, I have shown one part of the proof. Now I will show the other part of the proof. I must assume that and then show that P must be a point of concurrence.

Below is a GSP sketch of the triangle that is given.

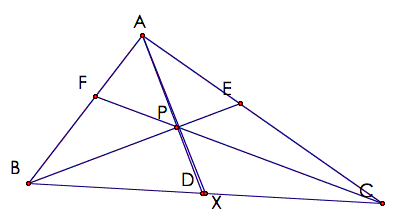
Assume that BE and CF intersect at P and AX has been constructed to go through P, but.

Since AD and AX both go through P, we know that and .

Then, by transitivity, .

After simplifying, I get .

So .

Hence, P is the point of concurrence of ,, and. Therefore, I have proved the theorem.

A question that arises is how might this theorem help us to prove concurrency of the lines of altitudes if P is the orthocenter?

First we need a sketch of when P is the orthocenter.

The theorem states that given a triangle, the three lines,, and intersect at point iff .

Let P be the orthocenter. Then, by definition of orthocenter, the lines through P from each vertex must be perpendicular to the sides of the triangle. Notice that Triangle ABD is similar to Triangle CBF by angle-angle similarity (they share the angle B and they each have a right angle by construction). Similarly (ha ha!), Triangle ACD is similar to Triangle BCE and Triangle BAE is similar to Triangle CAF. So the following proportions result:

, and

By Ceva’s Theorem, the three lines,, and intersect at point iff . Let’s assume that . Substituting values from above, gives us . Therefore, the altitudes must be concurrent.

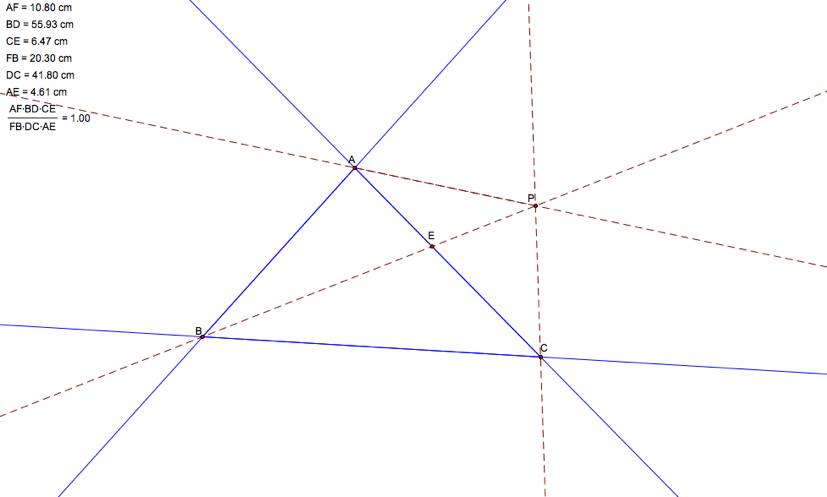
Next I will generalize my result so that the point P may be outside the triangle. In order to do that, I must extend the sides of the triangle to be lines. A working sketch of this case may be found here.

Return