Parametric Equations

 

By Thuy Nguyen

 

In this investigation we want to examine how the following sets of parametric equations behave when a = b, a < b, and a > b:

 

x = a(cos(t))ⁿ

y = b(sin(t))ⁿ

for n = 1, 2, 3, … and 0 £ t £ 2p.

 

We will begin with n = 1. Then our parametric equations are

 

x = acos(t)

y = bsin(t)

 

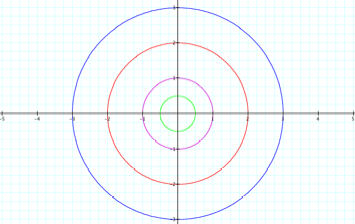
When a = b, our graph will be a circle centered at (0,0) with radius a (= radius b). The following graph shows how the parametric equations behave for a = b = -½, 1, 2, 3.

 

 

Now let’s see what happens when a < b. We will set b = 5 and vary a = -3, ½, 1, 2. We then get the following:

 

 

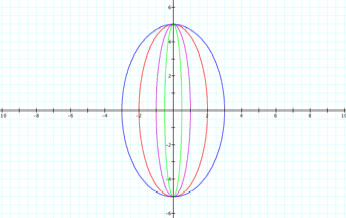
Conclusion (a<b):

The graph is that of an ellipse with the major axis extending from y = - |b| to y = |b| and the minor axis extending from x = -|a| to x = |a|.

 

Let’s see what happens when we fix a = 5 and vary b = -3, ½, 1, 2:

 

 

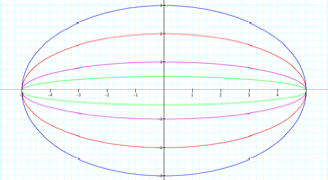
Conclusion (a>b):

The graph is that of an ellipse with the major axis extending from x = -|a| to x = |a| and the minor axis extending from y = -|b| to y = |b|.

 

Now for n = 2, we get the following set of parametric equations:

 

x = a(cos(t))²

y = b(sin(t))²

 

When a = b = -3, -2, 1, 2, 3, in teal, purple, green, red, and blue respectively, we get the following:

 

 

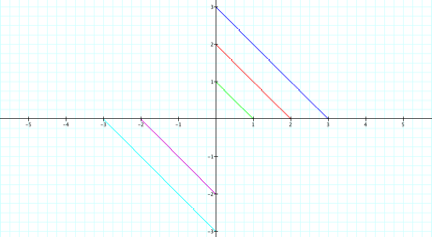
Conclusion (a=b):

We get line segments from x = a = b to y = a = b.

 

Now fix b = 5 and vary a = -1, ½, 1, 2, 3, in red, green, purple, blue, and teal respectively, to see what happens when a < b:

 

 

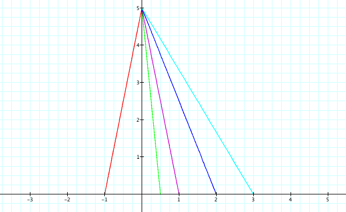
Conclusion (a<b):

We get line segments extending from the point (b,0) to the point (a,0).

 

Now fix a = 5 and vary b = -1, ½, 1, 2, 3 in red, green, purple, blue, and teal respectively to see what happens when a > b:

 

 

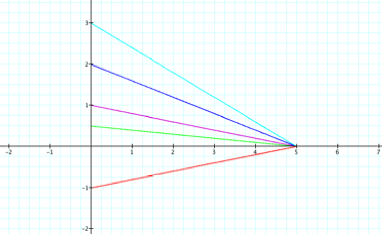
Conclusion (a>b):

We get line segments extending from the point (0,b) to the point (a,0).

 

For n = 3, we have parametric equations:

 

x = a(cos(t))³

y = b(sin(t))³

 

a = b = 1, 2, 3, 5 in red, purple, blue, and teal respectively:

 

 

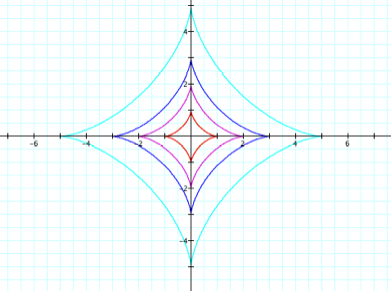
Conclusion (a=b):

We get closed curves with four “vertices,” at (0,a), (-a,0), (0, -a), and (a,0).

 

Now fix b = 5 and vary a = ½, 1, 2, 3 in green, purple, blue, and teal respectively:

 

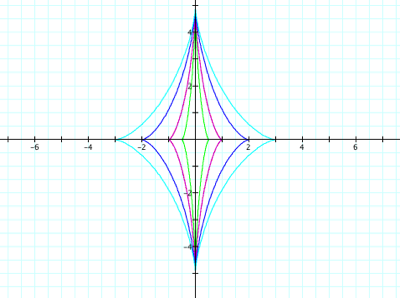
Conclusion (a<b):

We get closed curves with four “vertices” at (0,b), (-a,0), (0,-b), and (a,0).

 

Now fix a = 5 and vary b = ½, 1, 2, 3 in green, purple, blue, and teal respectively:

 

 

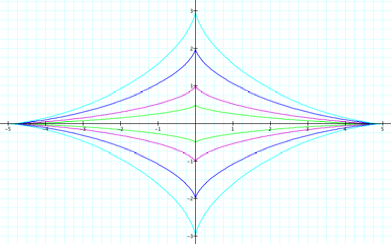
Conclusion (a>b):

We get closed curves with four “vertices” at (0,b), (a,0), (0,-b), and (a,0).

 

The following are graphs of our parametric equations for various n:

 

 

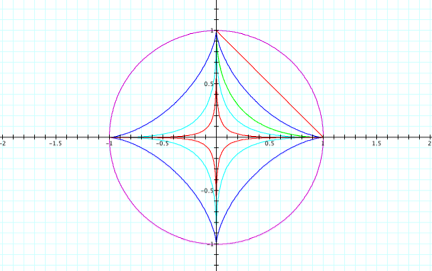
Conclusion for n > 3:

 

We get closed curves with vertices at (0,b), (a,0), (0,-b), and (a,0), but as n increases the curves get closer and closer to each other.

 

 

Return