Exploration of Polar Coordinates

By Thuy Nguyen

In this exploration we would like to explore the following five parametric equations:

I. r = 2asin(kq)

II. r = 2acos(kq)

III. r = 2acos(kq) + b

IV. r = 2asin(kq) + b

V. r = c / [acos(kq) + bsin(kq)]

Our goal is to generalize the graphs that these equations will produce with different values of a, b, c, and k.

Note: Although all polar coordinates are of the form (r, q), we will use the x-axis and y-axis in describing our graphs.

I. r = 2asin(kq)

Fixing k = 1

red: a = 1

purple: a = 2

blue: a = -1/2

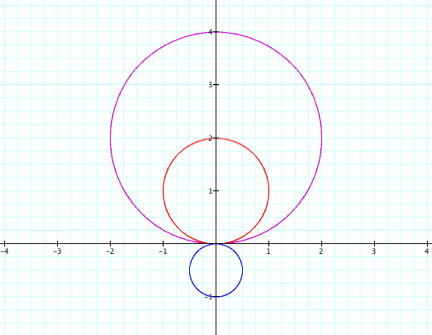
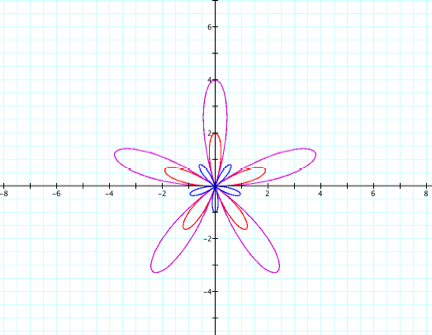
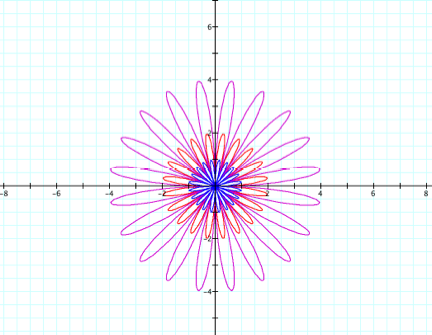
Now let k be an integer. We then have the following pattern:

- If k is odd, there are k petals

- If k is even, there are 2k petals

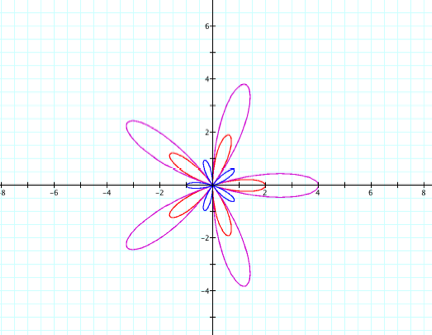
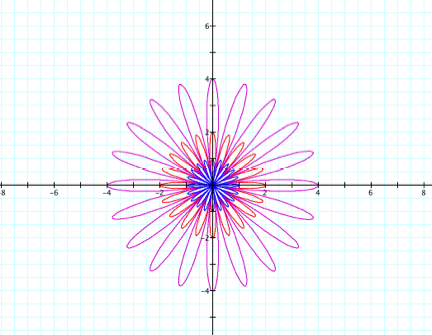
The following are graphs for k = 5 and k = 10, respectively, with the same a values as above.

II. r = 2acos(kq)

Again, fixing k = 1

red: a = 1

purple: a = 2

blue: a = -1/2

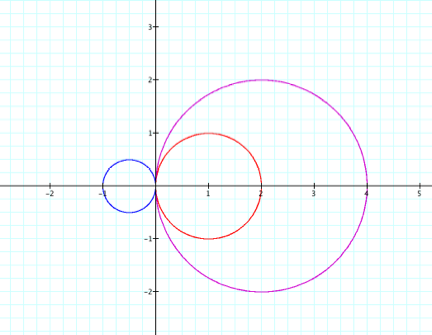
For integers k, we have the same pattern as in the case above, but the petals are in different positions.

III. r = 2acos(kq) + b

For the following graph, fix k = b = 1 and vary the a values.

Red: a = 0

Purple: a = 0.3

Blue: a = 0.5

Green: a = 0.9

Now vary a = 1, 2, 3, 4 in red, purple, blue, and green respectively.

We see that as a increases, the function gets larger in size and the inside loop gets closer to the outside loop. For negative a values, function is reflected across the y-axis.

IV. r = 2asin(kq) + b

We begin by varying the values of a just as we did previously and set b=k=1:

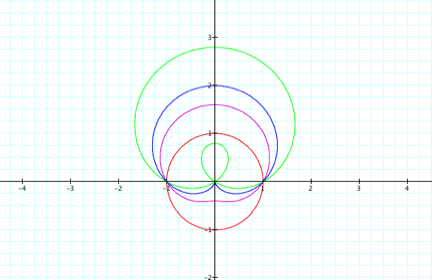
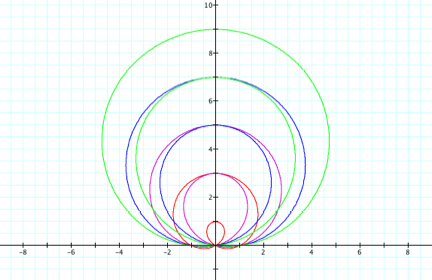
We see in the graphs above that we obtain the same graphs as the ones produced by varying a in part II, but this time the graphs are rotated 90 degrees counterclockwise. Now fix k = a = 1 and vary b = 1, 2, 3, 4: (negative b values are the same as positive b values)

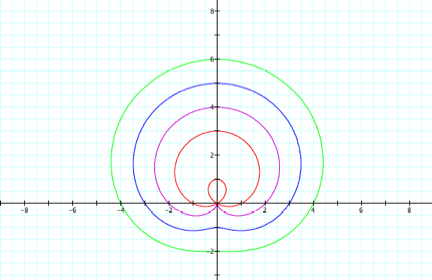
We already know what the graph looks like when a=b=k=1 (in red above), so we’ll start with k = 2:

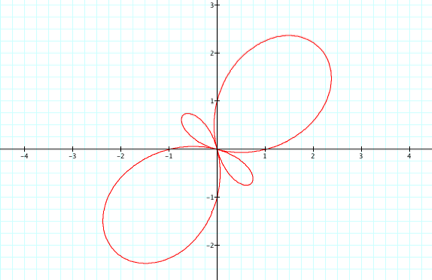
Now let’s look to see what happens when k = 6:

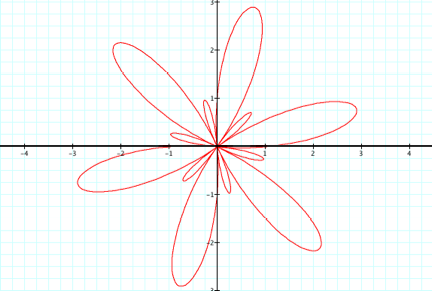
We see that there are 6 large and 6 small petals, a total of 12 petals. Let’s now try an odd k value, say k = 11:

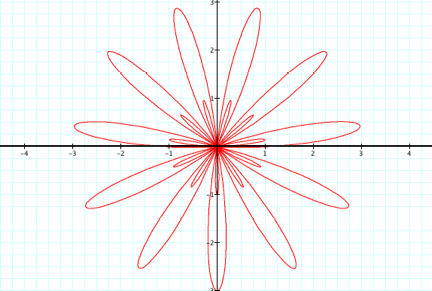
We see here that there are 11 large and 11 small petals, a total 22 petals, but notice that this time the small petals are inside the large petals.

Conclusion: For any nonzero positive integer k, then:

1. If k is odd, then the graph of the parametric equation r = 2asin(kq) + b (with b = a = 1) yields 2k petals, k of which are inside the other k larger petals.
2. If k is even, then the graph of the parametric equation r = 2asin(kq) + b (with b = a = 1) yields 2k petals, where the k smaller petals are not contained inside the larger petals.

For k = 0, we get a circle of radius b, and for k non-positive, reflect the graph over the x-axis.

V. r = c / [acos(kq) + bsin(kq)]

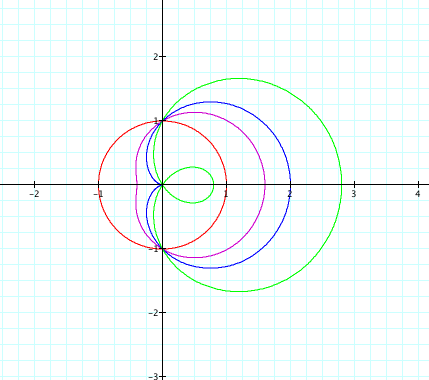
Let us first fix b = k = 1 and vary the values of a and c:

In the following graph,

Red line: a = 1, c = 1

Purple line: a = 2, c = 1

Blue line: a = 3, c = 5

Green line: a = 3, c = -5

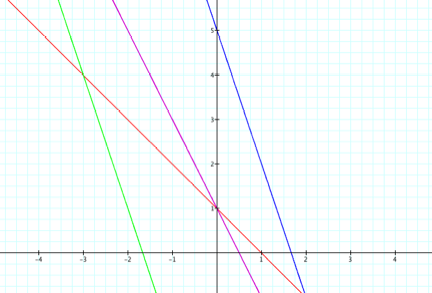
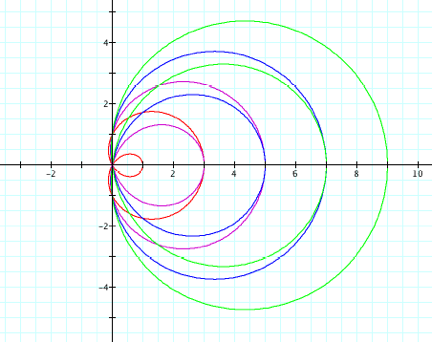
We see that the line always intersects the y-axis at y = c and it intersects the x-axis at c/a. Now we will use the same values of a and c as above, but we’ll now vary b as well.

In the following graph,

Red line: a = 1, c = 1, b = -1

Purple line: a = 2, c = 1, b = 1/2

Blue line: a = 3, c = 5, b = 2

Green line: a = 3, c = -5, b = 3

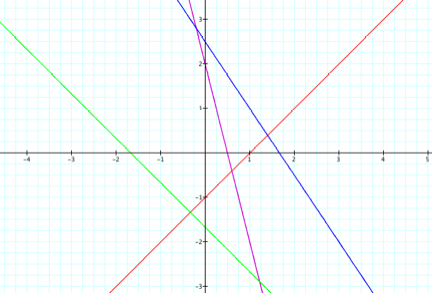
We see that the lines still intersect the x-axis at c/b, but now they intersect the y-axis at c/b.

The only value we have left to vary is k. Let’s first examine what happens when k is an odd integer. We’ll let a, b, and c be the same values as the function in red, so a = 1, c = 1, b = -1, and let k = 3:

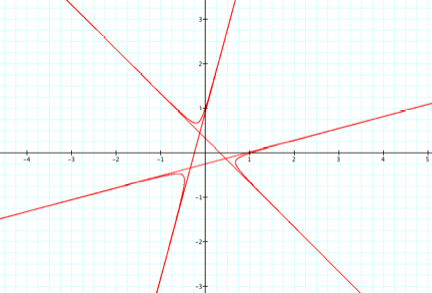
And now for k = 4, an even integer:

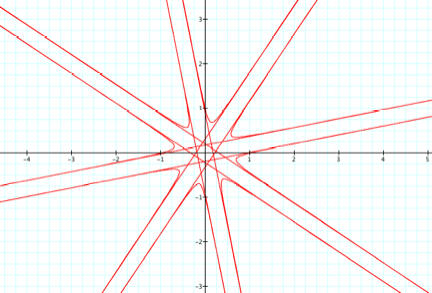
Conclusion:

In the parametric equation r = c / (acos(kq) + bsin(kq)) we have that for any nonzero integer k, if k is even, then the parametric equation yields 2k non-intersecting curves, and exactly one of these curves intersect the x-axis at x = c/a, exactly one (different from the first) intersects the x-axis at x = -c/a, exactly one intersects the y-axis at y = c/a, and exactly one intersects the y axis at y = -c/a, where a and c any nonzero real numbers. If k is odd, the equation yields k non-intersecting curves (for k = 1, we have a line), and exactly one of these curves will intersect the x-axis at either positive or negative c/b, and exactly one curve (different from the first) will intersect the y-axis at either positive or negative c/b, where b and c are nonzero real numbers. If one curve intersects an axis at a positive c/b, then the second curve must intersect the other axis at negative c/b, and vice versa.

Return