Locus of a Parabolic Function

 

By Thuy Nguyen

 

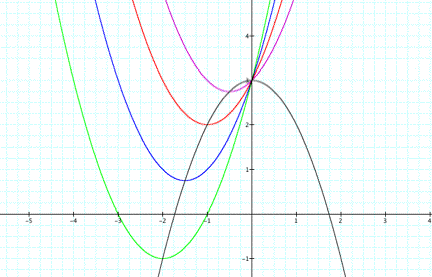
In this investigation we want to consider the locus of the vertices of the set of parabolas graphed from the function f(x) = x² + bx +1.

 

We want to show that the locus of the vertices of the set of parabolas graphed from f(x) = x² + bx +1 is the parabola g(x) = -x² + 1.

 

Let’s first examine the graphs of the function for b = -3, -2, -1, 0, 1, 2, 3:

 

 

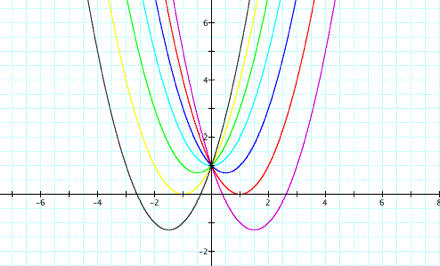
It will be useful for us to find the minimum for each of these parabolas, so let’s do so by first taking the derivative of f(x) and set it equal to zero:

 

f’(x) = 2x + b = 0

x = -b/2

 

Now substitute this back into f(x):

 

f(-b/2) = (-b/2)² + b(-b/2) + 1 = -b²/4 + 1

 

So the vertex of each parabola is at (-b/2,1 – b²/4).

 

Now let’s consider the function g(x) = -x² + 1:

 

 

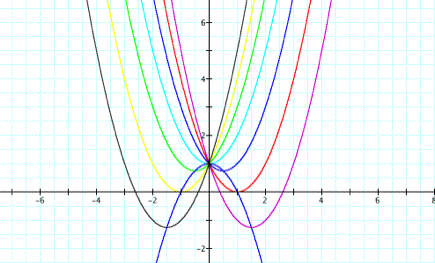
We notice that the parabola formed by this function seems to intersect each of the previous parabolas at its vertex. Let’s see if this is true:

 

f(x) = g(x) when

x² + bx + 1 = -x² + 1

2x = -b

x = -b/2

 

Substituting into g(x): g(-b/2) = -b²/4 + 1. Thus g(x) intersects each parabola at its vertex.

 

Generalization: The locus of the vertices of the set of parabolas graphed from y = x² + bx + c is the parabola y = -x² + c.

 

Here’s an example when c = 3:

 

 

 

Return