
Triangle and its Medians
By Thuy Nguyen
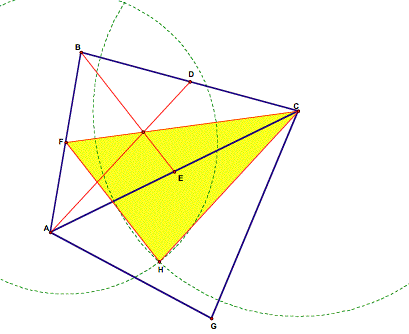
Construction of the median triangle:
- Start with triangle ABC and itŐs medians AD, BE, CF.
- We want to construct triangle AGC, which is congruent to triangle ABC and sharing side AC. We do this by constructing a circle with centered at A with radius AB and a circle centered at A with radius BC. These two circles intersect at a point B and at another point we will call G. Construct segments AG and CG to form the triangle AGC.

- Now we want to construct the median triangle. We do this by constructing a circle centered at F with radius BE and a circle centered at C with radius AD. We will call the intersection point of the two circles that lies inside triangle AGC H. Construct segments AH and GH. Triangle CFH is our median triangle. Click here for the GSP script on constructing the median triangle.
Lemma 1: The midsegments of a triangle divide the triangle into four congruent triangles. That is, they divide the triangle into four triangles of equal area.
Lemma 2: The medians of a triangle divide the triangle into six smaller triangles of equal area.
Claim: The area of the median triangle CFH is ¾ the area of the original triangle ABC.
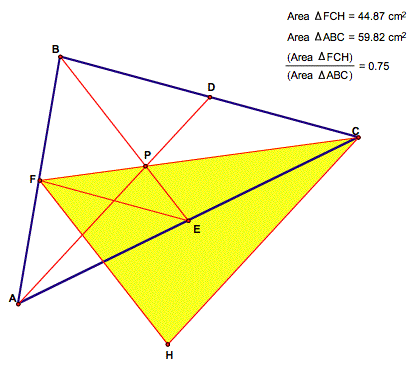
Proof:
Let A = area of ▲ABC. From lemma 2, we have that each of the six triangles formed by the medians have area equal to A/6.
Now construct segment EF. This is one midsegment of ▲ABC and hence ▲AFE has area of A/4 by lemma 1.
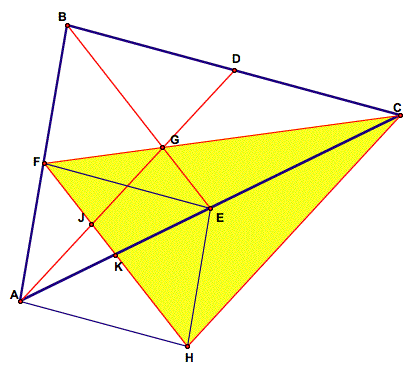
We have that segment FK is the midsegment of DBAE since F is the midpoint of segment AB and line FH is parallel to segment BE by construction. Then segments EK and KA are congruent and the areas of DAKF and DEKF are equal. Also since DAFE has area of A/4 and these two triangles partition it, DEKF has area of A/8.
Now we see that DAFG and DAGE from quadrilateral AFGE, whose area is A/3. If DAFK with area A/4 is removed, then DFGE remains with an area of A/12.
FK and KH are congruent since quadrilateral FAHE is a parallelogram. By construction, EH and FA are parallel, so <FHE is congruent to <AFH (alternate angles). Similarly, <HEB is congruent to <FAE. Thus DAKF and DEKH are congruent. So AF and EH are congruent.
Since segments AF and EH are parallel and congruent, quadrilateral FAHE is a parallelogram, making segment FK congruent to segment KH. Thus, DHKC has the same area as that of DFKC, 3A/8. Adding all the areas of these small triangles up, we have that the area of the median triangle is equal to 3A/4. QED.