Third Pedal Triangle

By Thuy Nguyen

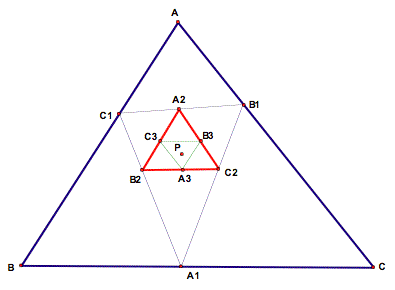
Theorem: The third pedal triangle is similar to the original triangle.

Click here for the GSP script for a general construction of a pedal triangle ABC where P is any point in the plane ABC.

Click here for the GSP script to see the third pedal triangle.

Proof:

We first note that P lies on the circumcircles of all the triangles AB₁C₁, A₂B₁C₂, A₂B₂C₁, and A₃B₂C₃. Now join P to every vertex on all four triangles. Then we have

<C₁AP = <C₁B₁P = <A₂B₁P = <A₂C₂P

= <B₃C₂P = <B₃A₃P

and

<PAB₁ = <PC₁B₁ = <PC₁A₂ = <PB₂A₂

= <PB₂C₃ = <PA₃C₃.

That is, the two pairs into which AP divides <A have their equal counterparts at B₁ and C₁, again at C₂ and B₂, and finally both at A₃. So ▲ABC and ▲A₃ B₃ C₃ have equal angles at A and A₃. Similarly, they have equal angles at B and B₃. QED.

Return