Final Project

By Thuy Nguyen

Part A: Bouncing Barney

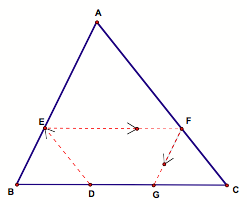
Barney is in a triangular room shown below. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB.

Claim: Barney will eventually return to his starting point.

Proof:

Let Barney’s starting point be at D (not the midpoint) on BC, then he walks in the manner described above to point E on AB, then F on AC, and G on BC. His path thus far forms two parallelograms BEFG and DEFC.

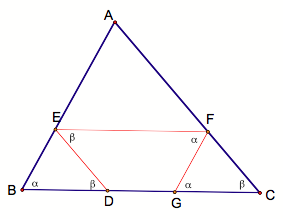
We see that DBED and DGFC are congruent since…

The angle at EBD (call this a) is congruent to the angle at GFE since opposite angles in a parallelogram are congruent. Similarly, the angle at FCG (call this b) and the angle at DEF are congruent. By the Z-Principle, the angle at EDB is also equal to b and the angle at FGC is equal to a. Finally we have that segments ED and FC are congruent since they are opposite sides of parallelogram DEFC. Thus by Angle-Angle-Side we have that DBED and DGFC are congruent.

Now let Barney continue bouncing till he reaches point H on AB and then point I on AC. We see that after hitting the walls 5 times, Barney will be back to his starting point! Click here for the GSP Script.

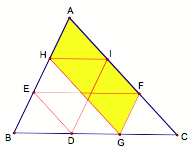
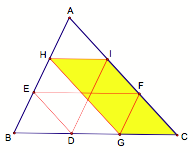
Once Barney is back to his starting point, we see that he has traced out two more parallelograms (shade above): FGHA and CGHI. Using the same argument as above, we have that DGFC and DHAI are congruent; hence, DBED and DHAI are also congruent. So we conclude that Barney must return to his starting point on his sixth path. If not, we will have a contradiction to the congruency of the triangles.

What happens if Barney starts out at the midpoint of side BC?

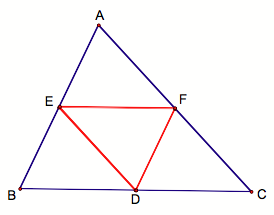
As shown in the figure above, Barney will need to travel only on three different paths before he reaches his starting point. The argument follows from the case when D is not the midpoint, where our first two parallelograms are BEFD and DEFC and our second two parallelograms are DEFC and DEAF. It follows that DBED, DDFC and DEAF are congruent.

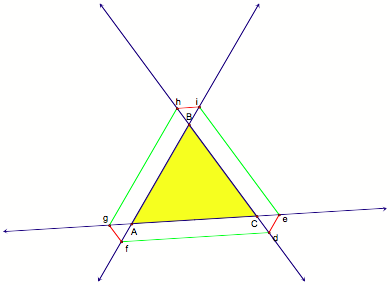
Our next question: What happens when Barney starts from a point exterior to segment BC? Click here for the GSP Script.

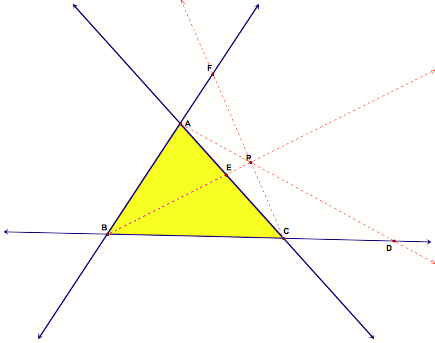
Part B

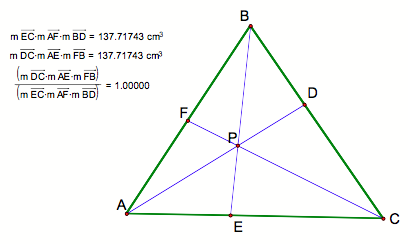
Ceva’s Theorem: If three segments AD, BE, CF, one through each vertex of a triangle ABC, are concurrent at point P, then

Click here for the GSP script.

Proof:

Recall that the areas of triangles with equal altitudes are proportional to the bases of the triangles. Referring to the figure above, we have:

Similarly,

So multiplying these will give us

QED.

Generalization: Ceva’s Theorem holds for any point p. That is, p can be outside of the triangle.

Click here for the GSP script to explore what happens when p is outside of the triangle.