Tree
Data
By
Gayle Gilbert & Greg Schmidt
In this problem we are given the following table of incomplete
information:
|
Age of
Tree |
100s
board feet |
|
|
|
|
20 |
1 |
|
40 |
6 |
|
60 |
|
|
80 |
33 |
|
100 |
56 |
|
120 |
88 |
|
140 |
|
|
160 |
182 |
|
180 |
|
|
200 |
320 |
We would like to use Excel To complete
the given table of information.
We begin by using the given
information to create a scatter plot graph, which gives us:
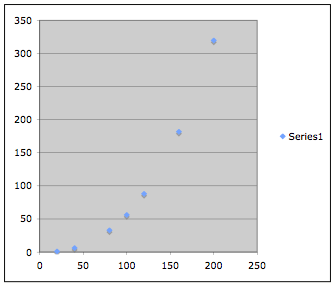
The scatter plot appears to closely
fit some power or exponential function.
We can click on the given graph when in Excel, and add a trend line to
the data points. The following
graph is the trend line for a power function:
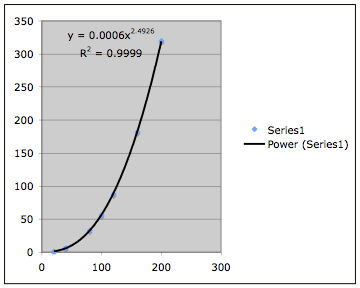
Our first
choice appears to fit the data points rather well, but we will also examine the
trend lines given when the exponential and polynomial fit is selected. Notice that Excel has also given us the
power function for the scatter points, which is 
. We also note
that the R squared value is given at 
, which indicates the power function strongly fits our data
points.
For the
polynomial trend line we have:
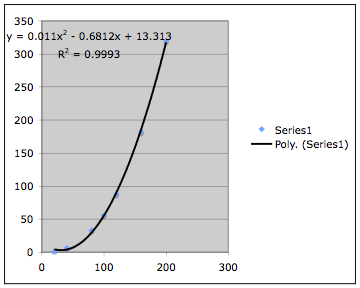
This also
appears to be a good fit, but we notice that Excel provides and R squared value
of 
, and so the polynomial function does not fit our data points
as well as the power function.
Finally, we
consider the exponential function fit to our data points.
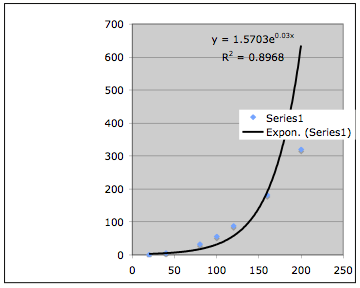
We immediately
see that this choice is not as good of a fit as the power function fit to our
data points.
Hence, we will
use the power function fit to our data points of 
to complete our
incomplete table.
So we have:
|
Age of
Tree |
100s
board feet |
|
|
|
|
20 |
1 |
|
40 |
6 |
|
60 |
16 |
|
80 |
33 |
|
100 |
56 |
|
120 |
88 |
|
140 |
134 |
|
160 |
182 |
|
180 |
251 |
|
200 |
320 |
How would this
differ if instead we used the polynomial function 
fit to our data
points?
Notice using
the given polynomial function to complete our table we have:
|
Age of
Tree |
100s
board feet |
|
|
|
|
20 |
1 |
|
40 |
6 |
|
60 |
12 |
|
80 |
33 |
|
100 |
56 |
|
120 |
88 |
|
140 |
134 |
|
160 |
182 |
|
180 |
247 |
|
200 |
320 |
So our tables
differ only for tree age 60 and 180Éso isnŐt that just dandy!