The
Locus of a Class of Parabolic Functions
by
Gayle Gilbert & Greg Schmidt
Problem: Consider the locus of the vertices of the set of parabolas graphed from
.
Show that the locus is the parabola
.
Consider 
, where 
, and the corresponding graphs:
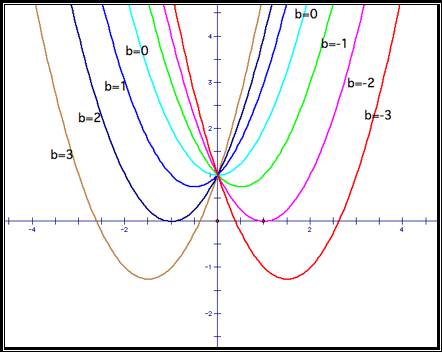
Now using calculus to find the minimum of each of the graphs we have for the minimum x-values:
,
since
.
Now, 
, and so we have that for each of our graphs
The minimum y-values of:
.
So for the vertex of each of our graphs is:
.
Now consider the function 
. By overlaying
it on our previously graphed functions we notice that it appears as though 
intersects every
graph at its vertex.
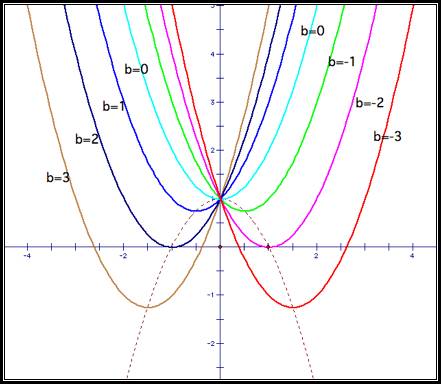
Indeed, this is the case. Consider again our general 
, and set it equal to 
.
So we have
.
Hence, 
intersects each 
at its
respective x-coordinate minimum.
Similarly, we check what we already suppose to be true, namely that
,
which is the y-minimum of each of our respective 
.
Whereby, we have shown that the locus of 
is given by the
function
.