
Tangent
Circles
by
Gayle Gilbert & Greg Schmidt
LetŐs make a GSP tool that will construct a circle tangent to the two given circles, A and B. (Note: we will start with one circle interior to the other circle.)
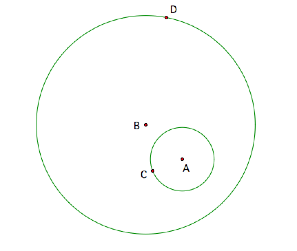
LetŐs construct line BD, where segment BD is the radius of the large circle.
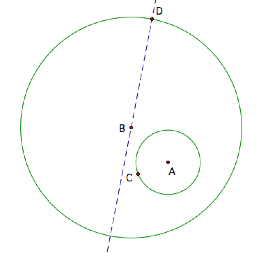
Next, construct circle D with radius AC.
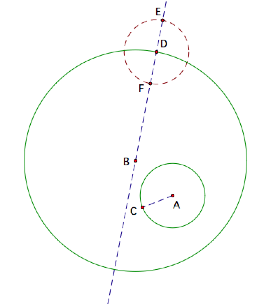
Construct segment AE and its perpendicular bisector. Note: where the perpendicular bisector and line BD intersect is point G, which will be the center of our Tangent Circle.
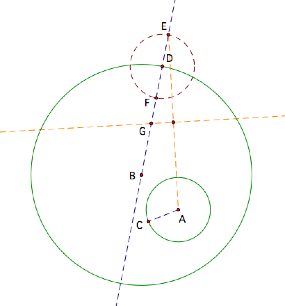
Finally, construct circle G with radius DG (this is the Tangent Circle).
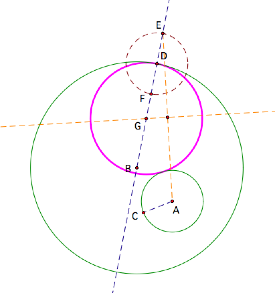
Notice the reason this works is that we now have an
isosceles triangle AGE, where AG![]() GE.
GE.
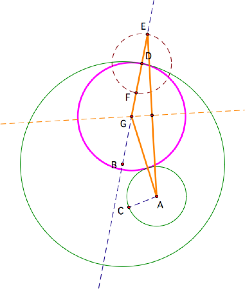
Notice the results if we had chosen to use point F instead of point E:
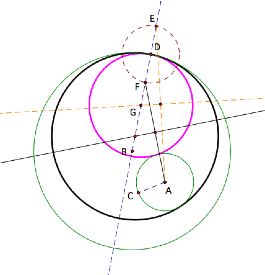
Now, letŐs explore the locus of points of the center of the tangent circles between the two given circles. You may use this tool during this exploration to make your own tangent circles. We will first explore the case when one circle is in the interior of the other circle. The red line gives us the locus of points.
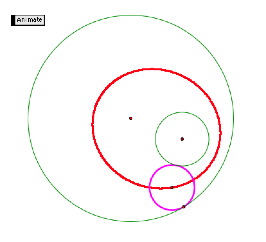
You can see that the locus of points look like they form an ellipse. We can check this conjecture by watching the distance between our loci (center of the two given circles) and foci (center of the tangent circle). Use this tool to construct two circles (one interior to the other), and watch how the distance stays constant as the tangent circle moves.
What happens when the two given triangles intersect? Do we still get an ellipse?
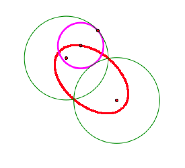
Yes, we do get an ellipse, and notice how the ellipse meets the two circles at their intersection points. This is because the tangent circle is going around the first circle until it minimizes to a single point at the point of intersection and then flips over to the other circle until it minimizes to a single point at the other point of intersection.
Finally, what happens in the last case when the second circle is created exterior to the first circle? Will we still get an ellipse?
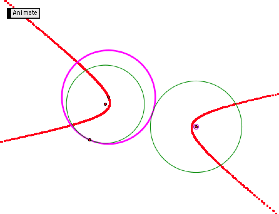
Instead of an ellipse, it looks like we have a hyperbola where the loci are the centers of our given circles and the focus is the center of the tangent circle. If it is a hyperbola, then the distance between the loci and the focus is always constant. LetŐs use this tool to construct two circles (one exterior to the other), and watch how the difference in the distances stays constant as the tangent circle moves.
Continue to explore tangent circles and see what you can discover.