Final Project:

In Search of

Bouncing Barney

And

Ceva’s Theorem

By

Greg Schmidt

Bouncing Barney:

Barney is in the triangular room shown here. He walks from a point BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB.

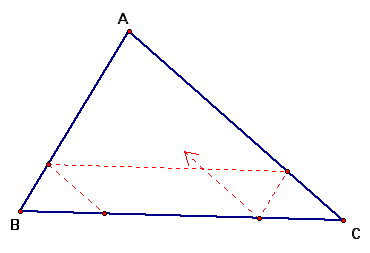
We will prove that Barney will eventually return to his starting point and show that he will return to this point after bouncing off a wall 6 times. Finally, we will discuss various starting points for Barney.

Click here for GSP script.

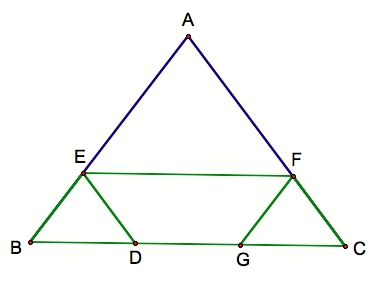
Let Barney start at an arbitrary point D (excluding the midpoint) on BC and let him travel parallel to AC to the point E on line AB. Let him continue traveling parallel to point F on AC, and on in a similar fashion to point G (as pictured above).

Now we note that thus far, Barney’s Bouncing about has formed two parallelograms, BEFG and DEFC.

Consider BEFG.

We note that the triangle EBD is congruent to the triangle FGC.

This follows from the fact that angle EBD is congruent to angle GFE, and the line segment BE is congruent to the line segment GF, since opposite sides and angles of parallelograms are congruent.

Similarly, considering DEFC we have that the angle FCG is congruent to angle DEF, and the line segment FC is congruent to the line segment ED.

Furthermore, since the line EF is parallel to the line BC, we have that angle DEF is congruent to angle EDB and angle GFE is congruent to angle FGC.

And so, angle EBD is congruent to angle FGC and angle FCG is congruent to EDB, by transitivity.

Hence, by the side angle postulate, triangle EBD is congruent to triangle FGC.

Letting go of Barney’s leash and allowing him to continue bouncing about we have the following:

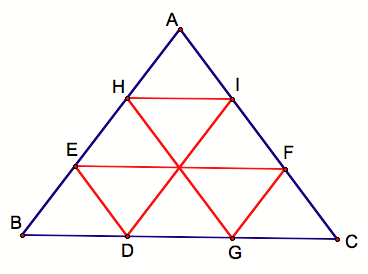
Imagine that: Barney has traced out another two parallelograms GHAF and HIGC.

Arguing as before we have that triangle FGC is congruent to triangle AHI and so triangle EBD is congruent to triangle FGC, which is congruent to triangle AHI.

Now for Barney’s last departure, we see he must arrive at point D since if not we would have a contradiction with respect to the congruence relations above.

So Barney bounces home on his sixth bounce!

When will Bouncing Barney stop?

We may never know!!!!

But at least we can always find him! We need only know how many times he has bounced.

We already know that if Barney has bounced 0 times he is at point D. If he has bounced exactly1 time: point E. If he has bounced exactly 2 times: point F. Exactly 3 bounces: point G. Exactly 4 bounces: point H. Exactly 5 bounces: point I. Exactly 6 bounces: point D (Barney is home at last!).

So we have the following relation for the nth bounce:

Barney will be at point:

D if .

E if .

F if .

G if .

H if .

I if .

We know that Barney will always return home on his 6^th bounce (or equivalently is nth bounce congruent modulo 6) as long as home is not the midpoint, since our point was arbitrarily chosen (excluding the midpoint).

So what happens if Barney starts at the midpoint? Well, we do not have to wait so long for Barney to come home. That is supposing he bounces at a constant rate.

Consider the following pictured path of Bouncy Barney:

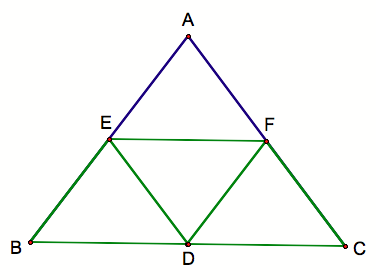
Now D, E, and F are all midpoints of BC, AB, and AC respectively since:

Line AB is parallel to line DF

Line BC is parallel to line EF

Line AC is parallel to line DE

So by the Alternate Interior and Corresponding Angle Theorem we know that each of the three triangles AEF, EBD, and FDC have corresponding congruent angles.

Therefore, all of the triangles are similar and so

BC = 2EF

AB = 2DF

AC= 2DE

Hence, we have that D, E, and F are midpoints, by the Mid-segment theorem.

And so when Barney starts to bounce about at one of the midpoints, he will return home on the 3^rd bounce. Again we could express his return with congruence relations as in the previous case. The only difference is we will now consider modulo 3.

The line segment joining a vertex of a triangle to any given point on the opposite side is called a cevian. Hence, if D, F, E are points on the respective sides BC, CA, AB of triangle ABC, the segments AE, BF, CE are cevians.

Ceva’s Theorem: If three cevians AE, BF, CE, one through each vertex of a triangle ABC, are concurrent, then

Proof:

Now, let ABC be any triangle. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

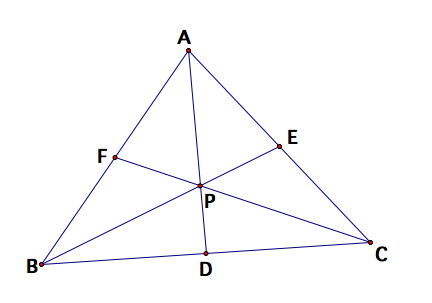
Now, saying that the three line segments are concurrent is the same thing as saying that all of the lines pass through on point, say P (as pictured above).

Next, we note that the areas of triangles with equal altitudes are proportional to the bases of the triangles. Just look at the pretty above and we can see that