1
Gregory Schmidt
Write up #1
Composition of the
Logarithmic and Exponential
Functions
Problem: Let 
and 
Consider:
(i)
(ii)
(iii)
(iv)
We will explore the graphs of our new functions, and explore the changes in the domains and ranges.
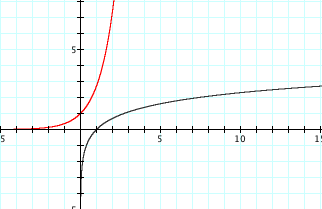
First we consider the graphs of 
and 
.
(1)
We see immediately, that 
and 
.
We notice that 
appears to
remain to the right of the y-axis, and 
appears to
remain above the x-axis.
Just a little thought reveals that in fact this must be the
case since for all 
, 
This is due to
the fact that 
, and so any power of 
must also be
greater than zero.
Now, for 
, we must first note how 
and 
are
related. When we talk about 
, we are really just asking what power of 
is equal to 
. That is, when
, what is 
?
For example, 
since 
implies that 
This
explains why 
is always to the
right of the y-axis, since 
for all 
. Hence, 
is not defined
for 
.
We say that the domain of 
, denoted 
and the range of
, denoted 
Similarly, 
and 
.
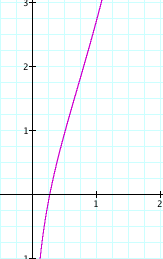
Now, 
, like 
, is always to the right of the y-axis.
(2)
Why?
Well, obviously 
if 
, since 
is not defined
for 
.
Hence, 
and 
.
We also not that 
lies between the
graphs of 
and 
, but this makes sense because we are simply adding the two
respective functions to form 
.
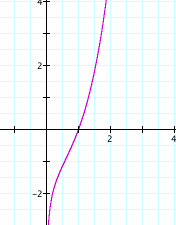
Now consider 
.
(3)
Again we see that 
and 
.
But this time the growth of 
eventually
overtakes 
. Just a little
thought we understand why this must be the case, since 
for all 
, and 
if 
.
What about 
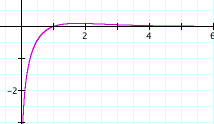
(4)
Well, as expected 
and 
.
What can we guess about 
and 
, where 
.
This time 
and 
.
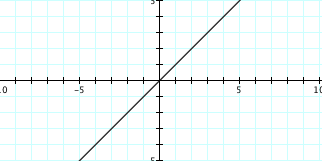
(5)
Notice: 
appears to be
very similar to the graph 
. Well, we need
only note that 
, and so 
, the identity function.
In this case, we say that 
and 
, and so 
.
