Unpacked
the Sine Function
Explore y =
R sin (Sx + T) + U
By Pei-Chun
Shih
In mathematics, the trigonometry is
the study of angles and triangles. Therefore, the trigonometry functions are
functions of an angle. There are two ways to define trigonometric functions.
The first one is to define them as ratios of the sides of a right triangle and
the second one is to define them using a unit circle.
The sine function is one of the
basic trigonometry functions. In a unit circle, if θ is an angle measured counterclockwise from the x-axis along
the arc, then sinθ is the
vertical coordinate of the arc endpoint. This explains why the sine function is
periodic with period of 2p. Other
properties of the sine function include:
1.
The graph of the sine function intercepts x-axis at np, where n
is an integer.
2.
The graph of the sine function intercepts y-axis at 0.
3.
The maximum values of the sine function are y = 1. It
occurs when x = 
+ 2np where n is
an integer.
4.
The minimum values of the sine function are y = -1. It
occurs when x = 
+ 2np where n is
an integer.
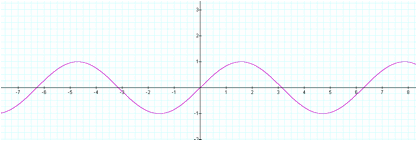
[y
= sin (x)]
Here I am going to examine graphs
of the trigonometric sine function: y = R sin (Sx + T) + U for different values
of R, S, T, and U.
Given R and S fixed at 1 and U
equals 0 and evaluate y = sin (x + T)
when T equals 0, ±1, and ±2.
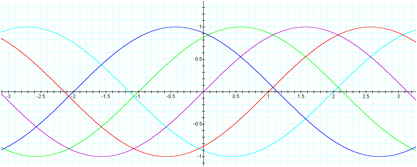
[sin (x), sin (x+1), sin (x-1), sin (x+2),
and sin (x-2)]
From the graph above, we can see
that the sine function translated horizontally. A horizontal translation of a
trigonometric function is called a phase shift. When T > 0, the
shift is to the left and when T < 0, the shift is to the right. The value of
the phase shift is determined by the value of T when the other two variables R,
S are fixed at 1.
More generally, consider the
algebraic form of the sine function: y = R sin (Sx + T), where R, S, T0. In order to solve this function for x, we need to
assign a zero to y for which R sin (Sx + T) = 0. Therefore, sin (Sx + T) = 0. It then follows that Sx
+ T = 0 since sin (0) = 0. Then we get x = -
. Therefore, y = 0 when x = -
. The phase shift value equals -
. From this we can make a conclusion for the phase shift:
when T > 0, the graph y = R sin (Sx) shifts to the left for |
| to form a new equation of y = R sin (Sx + T); when T <
0, the graph y = R sin (Sx) shifts to the right for |
| to form a new equation of y = R sin (Sx + T).
Given R and S fixed at 1 and T
equals 0 and evaluate y = sin (x) + U
when U equals 0, ±1, and ±2.
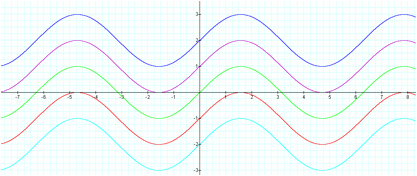
[sin
(x), sin (x)+1, sin (x)-1, sin (x)+2,
and sin (x)-2]
When a constant is added to a sine
function, the graph is shifted vertically. The value of the vertical shift is U. When U > 0, the
graph shifts upward and vice versa. Furthermore, the horizontal axis, which the
graph oscillates, shifts, too. The new reference line for the graph y = R sin
(Sx) + U is the equation y = U.
Let S = 1, T and U equal 0 and examine
the equation of the form y = R sin (x)
when R > 0.
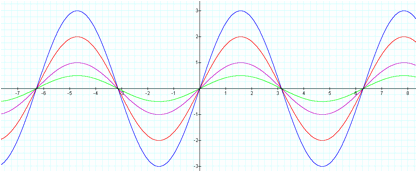
[sin (x), 1/2sin (x), 2sin (x), and 3sin (x)]
From the graph above, we can
observe the vertical expanding and compressing of the parent graph (y = sin x)
of the sine functions. Consider an equation of the form y = R sin (x) (R >
0). When R is a number larger than one, the graph vertically expanded compare
to the parent graph. When R is a number small than one, the graph vertically
compressed. Since the maximum absolute value of sin (x) is 1, the maximum value
of R sin (x) is |R| and is called the amplitude of y = R sin (x).
Here we were talking about the
situations when R is bigger than zero. What happens when R is smaller than
zero? If R is negative, the graph of the sine function upside down as comparing
to the graph showed above (see the graph below). However, the amplitude of y =
-R sin (x) remains the same as y = R sin (x).
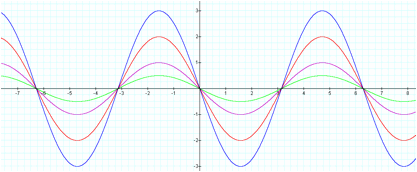
[-sin (x), -1/2sin (x), -2sin
(x), and -3sin (x)]
Let us examine our last variable,
S, given R equals 1 and T, U equal 0 and examine the equation of the form y = sin (Sx).
Let S be any positive number first.
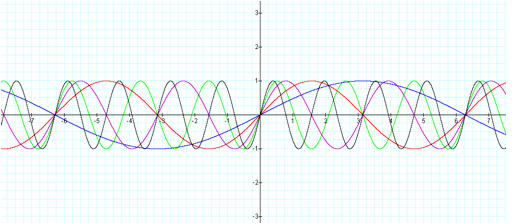
[sin (x),
sin (1/2x), sin (2x),
sin (3x), and sin (4x)]
Here we see the horizontal
expanding and compressing of the parent graph (y = sin x) of the sine functions.
Consider an equation of the form y = sin (Sx) (S >
0). When S is a number larger than one, the graph horizontally compressed
compare to the parent graph. When R is a number small than one, the graph
horizontally expanded. Since the period of the sine function is 2p, then y =
sin (Sx) can be written as y = sin (Sx + 2p) according
to the definition of periodic function. By the algebraic transformation, we can
get
y = sin S(x
+ 
). Therefore, the period of y = sin (Sx)
is 
, where S > 0.
LetÕs discuss about the situations
when S is smaller than zero. Just like our observations of negative number R
above, the graph of the sine function upside down as comparing to the graph
shown above (see the graph below). However, the period of y = sin (-Sx), which equals 
, remains the same as y = sin (Sx).
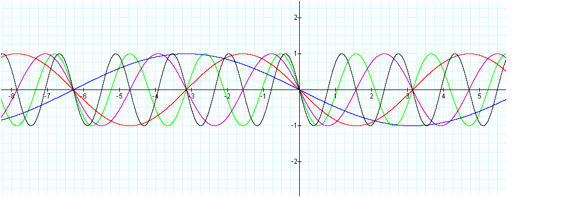
[sin
(-x), sin (-1/2x), sin (-2x), sin (-3x),
and sin (-4x)]
The exploration of the sine
function, y = R sin (Sx + T) + U, enables us to have a clearer understanding
about its translation, amplitude and period. Next time when seeing a complicate
sine function, y = 1.8 sin (
x - 8) + 3.3, as shown below
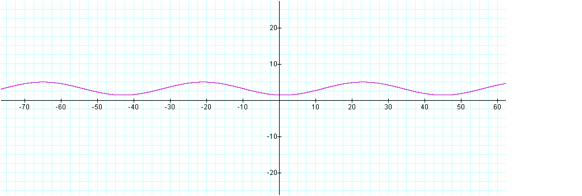
[y
= 1.8 sin (1/7x - 8) + 3.3]
You will know that the phase shift
of this graph equals -
= -(-8)/(
) = 56 units (where T = -8 and S = 
). The vertical shift is 3.3 upward (since U = 3.3 > 0),
the amplitude is |1.8|, and the period is
= 2p/(
) = 14p.
Conversely, you can write an equation of a sine function with amplitude,
period, phase shift, and vertical shift being given. That is to say, you have
to find the values of R, S, T, and U and substitute them into the equation y = R
sin (Sx + T) + U.