
Detaching Parabolas
Exploration of y = ax2 + bx + c
By Pei-Chun Shih
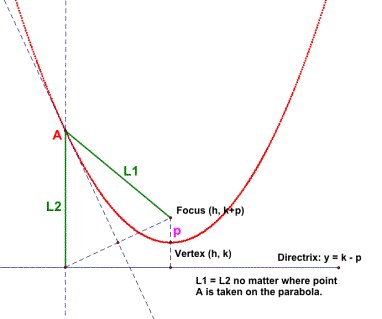
A
parabola is defined as follows: for a given point, called the focus, and a
given line not through the focus, called the directrix, a parabola is the locus
of points such that the distance to the focus equals the distance to the
directrix.
Click HERE to play with the animation file of a parabola.
The
axis of a parabola can be grouped into two categories. One is the vertical axis
of symmetry and the other is the horizontal axis of symmetry. The standard form
of the equation of a parabola with a vertical axis of symmetry can be written
as (x - h)2 = 4p (y - k), where (h, k) is the vertex, (h, k + p) is
the focus, x = h is the axis of symmetry, and y = k – p is the directrix.
Note that the parabola opens upward if p > 0 and opens downward if p < 0.
The equation of a parabola with horizontal axis of symmetry can be obtained by
switching the terms in the parentheses of the previous equation and get (y - k)2
= 4p (x - h) where (h, k) is the vertex, (h + p, k) is the focus, y = k is the
axis of symmetry, and x = h – p is the directrix. The parabola opens to
the right when p is positive, and it opens to the left when p is negative.
Here
I am going to explore the equation of y = ax2 + bx + c
for various a, b, and c. We will explore the effects of each coefficient by
fixing the other two and noticing the differences. This equation can be viewed
as an equation of a parabola with vertical axis of symmetry since the equations
(x - h)2 = 4p (y - k) and y = ax2 + bx + c
are equivalent
when
a =![]() , b =
, b =![]() , and c =
, and c =![]() + k.
+ k.
Let b = 1, c = 1 and vary the value of a (y = ax2 + x + 1):
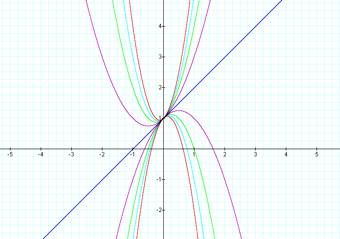
[y = ax2 + x + 1 when a = 0, ±1, ±2, ±3, and ±4]
All
the parabolas above are tangent each other at (0, 1). We can verify it by
solving the equations in pairs. For example, by solving y = 4x2 + x
+ 1 and y = -2x2 + x + 1 we can get the root of (0, 1). Any equations
of parabolas with the same coefficients in both the x and constant term are
tangent at the same point. Besides,
the coefficient of the x2 term, a, determines the direction of opening of a parabola. If
a is a positive number,
then the parabola is opening up and vice versa. a
also determines the width of a parabola. A parabola with larger absolute
value of a has narrower
opening than a parabola with smaller absolute value of a. The
last, note that when a = 0 the equation, y = x + 1, is not a parabola.
Therefore, we can get a conclusion that the equation of a parabola must have
one squared term.
Let a = 1, c = 1 and vary the value of b (y = x2 + bx + 1):
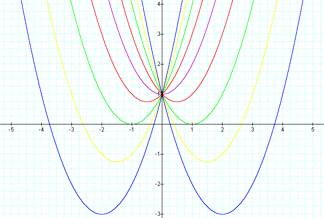
[y = x2 + bx + 1 when b = 0, ±1, ±2, ±3, and ±4]
From
the graphics above, we can see that all the parabolas intersect y-axis in the
same point (0, 1) since the y value of the equation y = x2 + bx + 1
always equals 1 when x equals 0. The parabolas descend below the x-axis with
the increase of the absolute values of b. Therefore, the coefficient of the x term, b, of the equation y = ax2 + bx + c
dominates the location of the parabolaÕs vertex. Here is the table that shows the relationships of the
parabolaÕs vertex with different b values:
|
b |
Equation |
Standard form of the equation |
Vertex |
|
0 |
y = x2 + 1 |
(x-0)2 = 4* |
(0, 1) |
|
1 |
y = x2 + x + 1 |
(x+ |
(- |
|
-1 |
y = x2 -x + 1 |
(x- |
( |
|
2 |
y = x2 + 2x + 1 |
(x+1)2 = 4* |
(-1, 0) |
|
-2 |
y = x2 -2x + 1 |
(x-1)2 = 4* |
(1, 0) |
|
3 |
y = x2 + 3x + 1 |
(x+ |
(- |
|
-3 |
y = x2 -3x + 1 |
(x- |
( |
|
4 |
y = x2 + 4x + 1 |
(x+2)2 = 4* |
(-2, -3) |
|
-4 |
y = x2 -4x + 1 |
(x-2)2 = 4* |
(2, -3) |
We
are surprisingly to discover that all the vertexes listed above fall on the
equation y = -x2 +1 which is a parabola opening downward. This suggests
that the locus of the vertices of the set of parabolas graphed from y = x2
+ bx + 1 is the locus of the parabola y = -x2 + 1. LetÕs draw a
graph to connect the vertexes of the parabolas listed above to support this
conclusion:
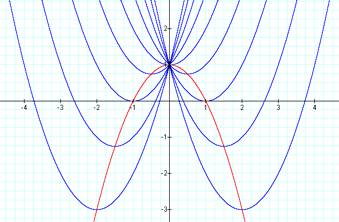
It
seems that this discover can be generalized. I will explore more about this in
the next write-up.
Let a = 1, b = 1 and vary the value of c (y = x2 + x + c):
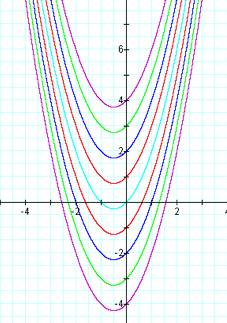
[y = x2 + x + c when c = 0, ±1, ±2, ±3, and ±4]
Here
the variance of c doesnÕt change the shape of a parabola, it changes the
vertical distance of a parabola
instead. As the absolute value of c becomes larger, the vertical distance of a parabola from x-axis
becomes longer. The point where a parabola intercepts y-axis is (0, c).
After
exploring the variables a, b, and c of the equation y = ax2
+ bx + c we know that a dominates a parabolaÕs opening direction and width, b determines the location of a parabolaÕs vertex, and c changes the vertical distance of a parabola.