Locus of the Vertices of Parabolas
The relationship between y = ax2 + bx + c
and y = -ax2 + c
By Pei-Chun Shih
From
the previous write-up, we found that the locus of the vertices of the set of
parabolas graphed from y = x2 + bx + 1 is the locus of the
parabola y = -x2 + 1:
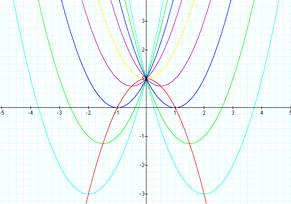
[The red parabola, y = - x2 + 1, connects
the vertices of the rest parabolas]
It
looks like there exists relationship between the equation y = ax2 + bx + c
and the equation y = -ax2
+ c. But before making any
conclusion, I will do several more explorations to support my argument.
y =
2x2 + bx + 1 & y = -2x2 + 1 (let a = 2, c = 1 and vary the value of b):
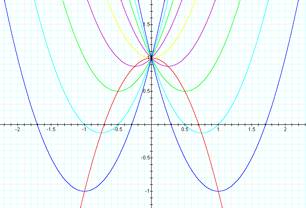
The
equation y = -2x2 + 1 passes through the following points: (-1, -1),
(1, -1), (-0.75, -0.125), (0.75, -0.125), (-0.5, 0.5), (0.5, 0.5), (-0.25,
0.875), (0.25, 0.875), and (0, 1) which are the vertices of the parabolas of
equation y = 2x2 + bx + 1, with b = 0, ±1, ±2, ±3, and ±4.
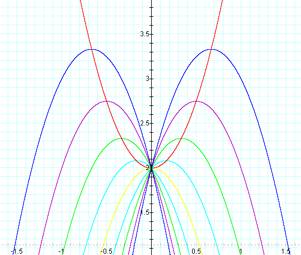
y =
-3x2 + bx + 2 & y = 3x2 + 2 (let a = -3, c = 2 and vary the value of b):
Again,
the equation y = 3x2 + 2 passes through the points which are the
vertices of the parabolas of equation y = -3x2 + bx + 2, with b = 0,
±1, ±2, ±3, and ±4.
Therefore,
we can generalize the equation of the locus, for any equation of the form y = ax2 + bx + c
as the equation of:
y =
-ax2 + c.
Well,
generalizing by graphics along is not complete enough for a rigorous proof in
mathematics. Therefore, here I am going to use algebra to prove the
relationship between the equations of y = ax2 + bx + c
and y = -ax2 + c.
As I
have discussed in my previous write-up 2 that the standard form of the equation
of a parabola with a vertical axis of symmetry can be written as (x - h)2
= 4p (y - k), where (h, k) is the vertex, (h, k + p) is the focus, x = h is the
axis of symmetry, and y = k – p is the directrix. Since we have known
that the equation, y = ax2
+ bx + c, represents a parabola with a vertical axis of symmetry,
it is reasonable to write it in the standard form of (x - h)2 = 4p
(y - k).
y =
ax2 + bx + c
ax2
+ bx = y – c
x2
+
x = 
(y – c)
x2
+ 2* x *
+ (
)2 = 
(y – c) + (
)2
(x+
)2 = 
(y – c+
)
(x+
)2 = 4*
[ y – (c -
)]
Therefore,
h = -
, k = c -
, and the vertex of y = ax2 + bx + c is (-
, c -
).
Since
we want to prove that every vertex from the equation y = ax2 + bx + c is also on the equation y = -ax2 + c, plug the vertex
(-
, c -
) into the equation y = -ax2 + c is the next step.
y =
-ax2 + c
Let
x = -
and y = c -
.
c -
= -a*(-
)2 + c
c -
= -
+ c
Thus,
0 = 0. This confirms that every point of the form (-
, c -
) is on the equation y = -ax2 + c.
By
the algebraic statement above, we have proved that the locus of the vertices of
the set of parabolas graphed from
y = ax2 + bx + c is the locus of the parabola y = -ax2 + c.