
The Fermat Point
By Pei-Chun Shih
In
this write-up, I am going to find a point inside a triangle ABC such that the
sum of the distances from this point to each of the three vertices is a
minimum. This point is called the Fermat point because the problem of finding a point minimizes the
sum of distances from vertices of a triangle was first raised by Fermat.
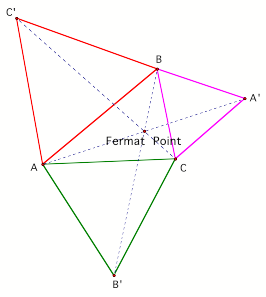
In
order to locate the Fermat point, three equilateral triangles out of the three
sides of the given triangle ABC need to be constructed first. Let AÕ, BÕ, and
CÕ be the apex of these three equilateral triangles. Then draw lines from AÕ to
A, BÕ to B, and CÕ to C. The point where these three lines intersect is the
Fermat point.
There
are several interesting properties about the Fermat point:
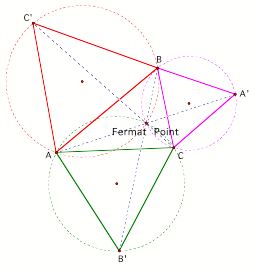
1.
The circumcircles of
these three equilateral triangles (triangle ABCÕ, ABÕC, and AÕBC) intersect at
the Fermat point.
2.
Let the Fermat point be
denoted as F. Then it can be proved easily that angle AFB, AFC, and BFC are all
equal to 120 degrees.
[Proof]: From the diagram above, A, F, B, CÕ are cyclic quadrilateral. So
opposite angles are supplementary which add up to 180 degrees. Since triangle
ABCÕ is an equilateral triangle, each interior angle equals 60 degrees.
Therefore, angle AFB, the opposite angle of angle ACÕB, equals 120 degrees
which is 180 degrees minus 60 degree. The same reasoning can be hold for angle
AFC and BFC.
3.
All the segments AAÕ,
BBÕ, and CCÕ have the same length.
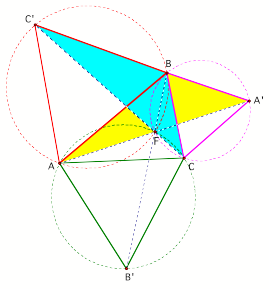
[Proof]: In order to prove that AAÕ equals CCÕ, we need to prove that triangle
BCCÕ is congruent to triangle BAÕA. Since triangle ABCÕ and BCAÕ are
equilateral triangles, then CÕB = AB, BAÕ = BC, and angle CÕBA = 60 degrees =
angle AÕBC. So angle CÕBC = angle CÕBA + angle ABC = angle CÕBC + angle ABC =
angle ABAÕ. Therefore, triangle BCCÕ and BAÕA are congruent by the
Side-Angle-Side congruence theorem. Thus, segment AAÕ equals segment CCÕ. We
can prove that BBÕ = CCÕ by the same reasoning.
Now,
itÕs the time to prove that point F is really the one we are looking for. That
is to say, point F is the point minimizes the sum of distances from vertices of
a triangle.
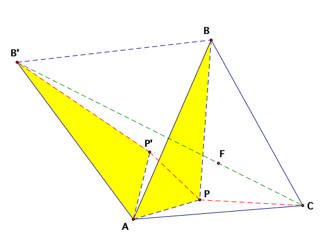
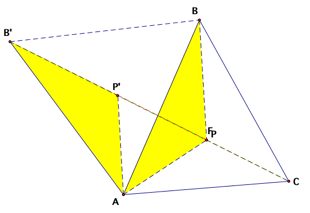
Click HERE if you want to move the point P to F by yourself.
In
the triangle ABC, select an arbitrary point P and connect it with vertices A,
B, and C. Use point A as a center to rotate the triangle BAP 60 degree into
position BÕAPÕ. Then triangle APPÕ is an equilateral triangle since PÕA = PA
and angle PÕAP is 60 degree. Hence, PA = PPÕ. Also, PB = PÕBÕ. Therefore, PA +
PB + BC can be written as PPÕ + PÕBÕ + PC which is a path from BÕ to C. Since
the shortest distance of two points is a straight line, then the path from BÕ
to C will be minimized if it is a straight line. In other words, when PÕ and P
lie on the segment BÕC the distance will be minimized (click on the animation
bottoms above to see the demonstrations). We can observe from the animation
that when P and F, the Fermat point we constructed earlier, are concurrent,
both P and PÕ lie on the segment BÕC. Therefore, the Fermat point, F, is the
point such that the sum of its distances from the vertices of a triangle is a
minimum. Furthermore, since point P and F are concurrent, angle BÕPC = angle
BÕFC = 180 degrees. So angle APC = angle AFC = 180 – angle AFPÕ = 180
– 60 = 120 degrees which is another way to prove that property 2
mentioned above is true.