
Tangent Circles
By Pei-Chun Shih
In
this write-up, I am going to use GSP to explore the relationships of a circle
tangent to two given circles.
Here
the circles c1, c2, and the point A are given. I want to construct a circle
tangent to both the circle c1 at the point A and the circle c2. The first step
is to construct a line through the given point A and the center, point O, of
the circle c1. Then create a circle with the center at the point A, which has
the same radius as the circle c2. Denote this circle as c3. Also denote the
intersection of the line AO and the circle c3 as B. Next, construct a segment
between points B and the center of the circle c2. Construct the perpendicular
bisector of the segment BQ and denote the intersection of the segment BQ and
the line AO as D. Use the point D as the center and AD as the radius to
construct a circle, which satisfies the criteria mentioned above.
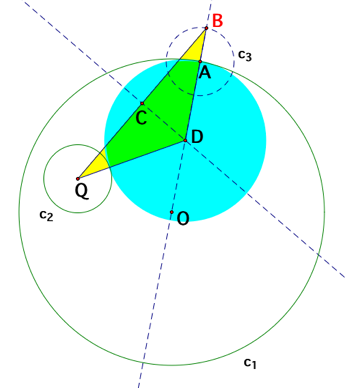
[Graph
A: The blue circle solid is
tangent to both c1 at A and c2]
The
following is another possibility for the desired circle to be tangent to both
c1 and c2. The concepts of constructing this circle are the same as above. The
only difference between the constructions here and those above is the location
of the point B where the line AD and the circle c3 intersect. The point B
chosen here is inside the
given circle c1 whereas the point B in the previous construction is outside the
circle c1.
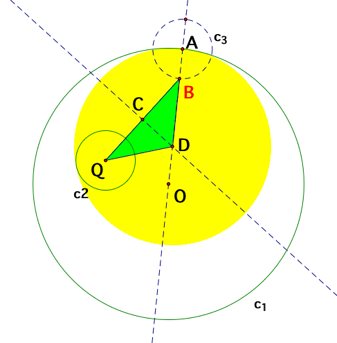
[Graph B: The yellow solid circle is tangent to both c1 at A and c2]
After
constructing the desired tangent circles, I am going to discuss the loci of the
centers of the two tangent circles just constructed.
[Graph C: The loci of the center D with the animation of the point A]
Click HERE to play with the animation file of the Graph C.
From
the Graph C above, it seems like the loci of the center D of the solid blue
circle form an ellipse. How to be sure that it is really an ellipse? By the
definition of ellipses, the sum of the distances from any point on the ellipse
to its two foci is constant. Since D is a point on the locus, if the sum of the
distances from D to Q and O is constant, then it is done. According to the
constructions earlier, the line CD is the perpendicular bisector of the segment
BQ. By the definition, the perpendicular bisector of a segment BQ is the set of
all points which are equidistant from B and Q. Therefore, the segments DQ and
DB are equal in length. So (DQ + DO) can be written as (DB + DO) which equals
the sum of the radii of the circle c1 and the circle c3. Since the circle c3 is
congruent to the circle c2, and both c1 and c2 are given circles, then the sum
of their radii wonÕt change no matter where the point A is on the circle
c1. Thus, the sum of the distances
from D to Q and O is constant which by definition proves that Q and O are the
foci of the ellipse formed by the loci of D.
How
about the loci of the center of the solid yellow tangent circle in the Graph B?
From the graph D below, it seems like it is also an ellipse. LetÕs prove it! By
the same reasoning presented earlier, since the line CD is the perpendicular
bisector of the segment BQ, then DB = DQ. Therefore, DQ + DO can be written as
DB + DO which also equals to AO – AB, the difference of the radii of the
circle c1 and c3. Since the circle c3 is congruent to the circle c2, and both
c1 and c2 are given circles, then the difference of their radii remains the
same no matter where the point A is on the circle c1. Hence, the sum of the distances from D to Q and O is
constant which by definition proves that Q and O are the foci of the ellipse
formed by the loci of D.
[Graph D: The loci of the center D with the animation of the point A]
Click HERE to play with the animation file of the Graph D.
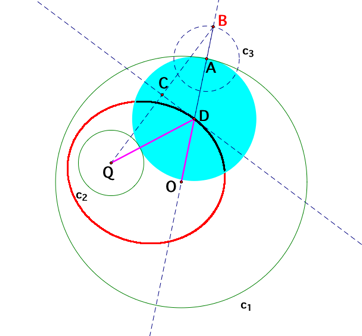
How
about when the two given circles intersect? Will the locus of the centers of
the constructed tangent circles still be ellipses? The loci formed by the
center of the solid blue circle in Graph A remain the shape of ellipse when the
two given circle, c1 and c2 intersect. Please see the Graph E below for the
diagram of the locus. The reasoning procedures of why it is an ellipse are the
same as those in the previous section. So there is no reason to repeat them
here.
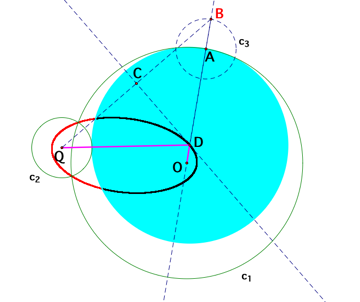
[Graph E: The loci of the center D with the animation
of the
point A when c1 and c2 are intersect]
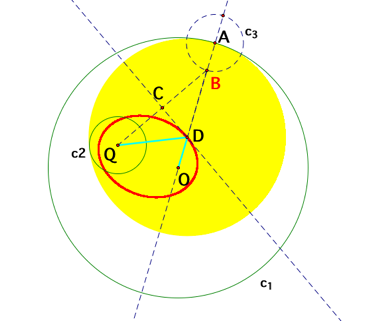
However,
when it comes to the loci of the center D of the solid yellow circle in Graph
B, the shape is not an ellipse anymore. According to the Graph F below, it
looks like the shape becomes a hyperbola when the two given circles intersect.
LetÕs check that the conjecture is correct!
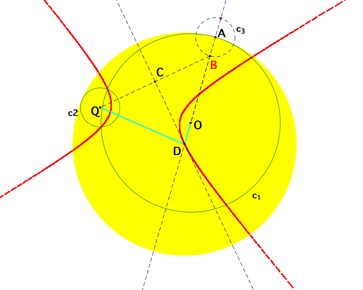
[Graph F: The loci of the center D with the animation
of the point A when c1 and c2 are intersect]
By
the definition, a hyperbola is the set of all points in the plane which the
difference of the distances from two foci is constant. Suppose that the points
O and Q are the foci of the hypothesized hyperbola, then the difference of DO
and DQ must be constant to fulfill the definition of hyperbola. Again, the line
CD is the perpendicular bisector of the segment BQ, and so DQ equals DB in
length. Therefore, (DQ – DO) can be written as (DB – DO) which
equals the length of BO. Since BO equals (AO – AB) which is the
difference of the radii of the circle c1 and c3, then BO is constant because c1
and c3, congruent to c2, are given circles. Hence, the difference of the
distances from D to Q and O is constant which by definition proves that Q and O
are the foci of the hyperbola formed by the loci of D.
How
about when the two given circles, c1 and c2, are disjoint? What are the shapes
of the locus of the centers of the constructed tangent circles?
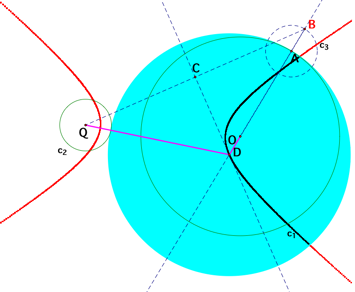
[Graph G: The loci of the center D with the animation
of the point A when c1 and c2 are disjoint]
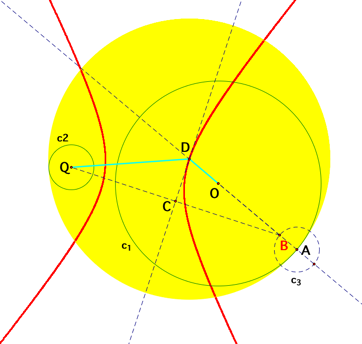
[Graph H: The loci of the center D with the animation
of the point A when c1 and c2 are disjoint]
It is obvious that the loci are hyperbolas according
to the Graph G and H above. Since the proofs are quite similar as those have
been done earlier, I would like to omit them here.
Lastly, it would be helpful to end this write-up by
applying what we have learned about the tangent circles so far in a question
like the construction of three circles tangent to each other in a single point.
Here are the settings:
Given a line and
a circle with center K. Take an arbitrary point P on the circle. Construct two
circles tangent to the given circle at P and tangent to the line.
First, construct a line that passes through the points
K and P. From the previous practices of constructing tangent circles, I get the
conclusion that the center of the desired tangent circle must lie on the line
that connects the center of the given circle and the given point. Therefore, the centers of the two
desired circles must lie on the line KP. Second, construct the line L passes
through the point P and is perpendicular to the line KP. The line L is tangent
to the circle c1 at the point P since P lies on both L and c1 and the radius KP
is perpendicular to L. Denote the intersection of the lines L and M as the
point A. Third, construct the circle c2 with the center at A and the length of
AP as its radius. The circle c2
intersects the line M at the points B and C. Fourth, connect BP and CP and
construct the perpendicular bisectors of the segments BP and CP. The
perpendicular bisectors of the segments BP and CP intersect the line KP at the
points D and E respectively. The last, use the points D and E as the centers
and DP and EP as the radii to construct the circles c3 and c4. Then c3 and c4
are the desired circles both tangent to the line M and tangent to the circle c1
at the point P.
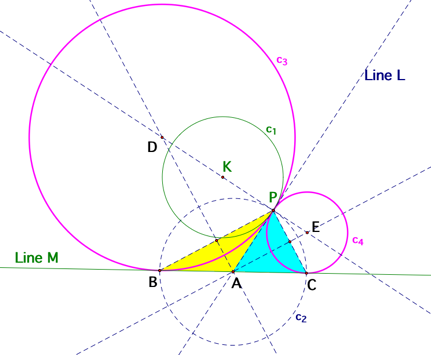
[Graph I: The circles c3 and c4 are both tangent to the
line M and tangent to the circle c1 at point P]