Altitudes and Orthocenters

By Pei-Chun Shih

The three altitudes of a triangle intersect in a single point, called the orthocenter of the triangle. The orthocenter lies inside the triangle if and only if the triangle is an acute triangle. There are several interesting relationships between the three altitudes and the orthocenter. Here I am going to use GSP to explore them and provide proofs of the relationships.

---

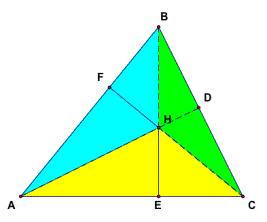
Construct the orthocenter H in a given acute triangle ABC. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully. Prove that

+ + = 1 and + + = 2.

The first proof can be accomplished by using the area formula of a triangle which is half of the product of a base and its corresponding altitude. Let’s divide the triangle ABC into three small triangles: AHC, BHC, and AHB. So the area of triangle ABC equals the sum triangles AHC, BHC, and AHB:

△AHC + △BHC + △AHB = △ABC

Divide each side by △ABC,

+ + = 1

Express by the area formula of a triangle,

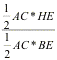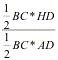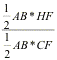+ + = 1

Simplify,

+ + = 1 (Proposition 1)

The second proof can be done by using the proposition 1 we have just proved above. Since BH = BE – HE, AH = AD – HD, and CH = CF – HF, then we can do the following substitution:

+ + = + +

Simplify,

= (1 - ) + (1 - ) + (1 - )

Rearrange,

= 3 – ( + + )

Substitute + + for 1 and we can get

+ + = 3 – 1 = 2.

We can explore the properties of the altitudes and orthocenters further by constructing the circumcircle of the triangle ABC and extending each altitude to its intersection with the circumcircle at corresponding points P, Q, and R.

There is a relationship between the altitudes and AP, BQ, and CR which is + + = 4. We can prove it by applying the proposition 1 again here. Before using the proposition 1, let’s add some construction lines first. Connect AR, BP, and QC. We want to prove that HD = PD, HE = QE, and HF = RF.

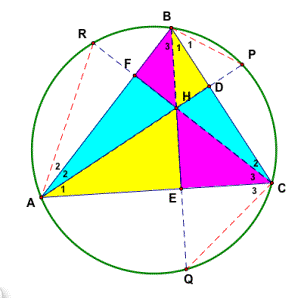
Consider △BHD and△AHE. △BHD and△AHE are similar triangles by the Angle-Angle Similarity Theorem since ∠BHD = ∠AHE and ∠BDH = 90 degrees = ∠AEH. Therefore, ∠HAE = ∠HBD. Since points A, E, C are collinear, points A, H, P are collinear, and points B, D, C are collinear, then ∠HAE = ∠PAC and ∠PBD = ∠PBC. ∠PAC = ∠PBC since they intercept the same arc PC. Hence, ∠PBD = ∠HBD. △BHD and△BPD are congruent triangles by the Angle-Side-Angle Congruence Theorem since ∠PBD = ∠HBD, BD = BD, and ∠BDH = 90 degree = ∠BDP. Therefore, HD = PD. Similarly, we can get that HE = QE and HF = RF by performing the same steps above for △ARH and△CQH. Thus, AP = AD + PD = AD + HD, BQ = BE + QE = BE + HE, CR = CF + RF = CF + HF.

So, + + = + +

= (1 + ) + (1 + ) + (1 + )

= 3 + + +

= 3 + 1 by Proposition 1

= 4

Therefore, + + = 4.

RETURN