
Pedal Triangle & Simson Line
By Pei-Chun Shih
Given
a triangle ABC and a point P that is not one of the vertices of the triangle
ABC. A pedal triangle RST of a point P is the triangle formed by the three feet
of the perpendiculars from P to the lines containing the sides of the triangle
ABC. We call the point P the pedal point.
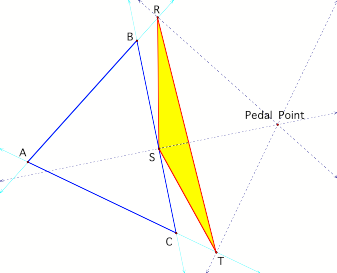
[Example when Pedal Point is outside the triangle ABC]
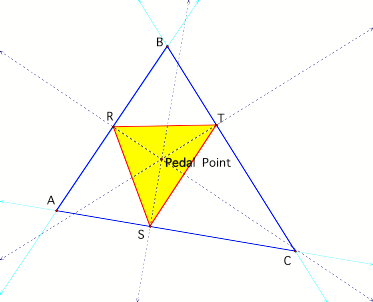
[Example when Pedal Point is inside the triangle ABC]
The
pedal point P can be any point in the plane, either outside or inside the
triangle ABC. However, the locations of the pedal point P relate to the given
triangle ABC exist some interesting relationships.
First,
let pedal point P be a point on the circumcircle of triangle ABC. Then the
three vertices of the pedal triangle RST are collinear. In other words, the
pedal triangle RST degenerates into a line. This line is known as the Simson
Line.
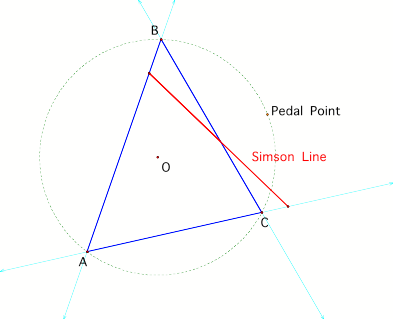
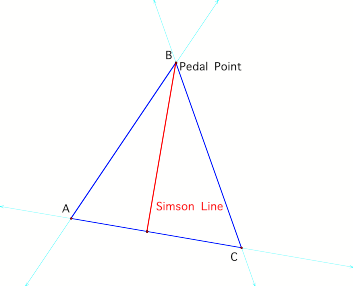
Second,
let pedal point P be one of the vertices of triangle ABC. The Simson Line of P
becomes the altitude of the triangle ABC with its foot on the side opposite to
the vertex where P is. Since the vertices of the triangle ABC are points on its
circumcircle, it makes sense that when P is concurrent with them, the pedal
triangle degenerates into a straight line as we explored earlier.
Third,
draw a line through the pedal point P which lies on the circumcircle of the
triangle ABC and the circumcenter O. When each of the vertices of the triangle
ABC is collinear with P and the circumcenter O, P has the sides of triangle ABC
as its Simson Line. That is to say, the Simson Line and the sides of the
triangle ABC are congruent if and only if the diameter of the circumcircle has
both P and one of the vertices of the triangle ABC on it.
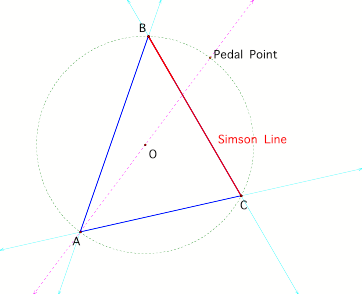
[When P, O, and A are collinear, side BC is the Simson
Line of P]
If
we trace the image of the Simson Line as the pedal point is moving along the circumcircle,
then we will find that the envelope formed by the Simson Line is a circular
hypocycloid.
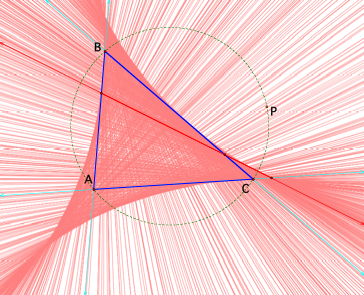
Here
I am going to find the locus of the midpoints of the sides of the pedal
triangle. First, locate the midpoints of the sides of the pedal triangle whose
pedal point (P2) is on the circumcircle of the triangle ABC. Trace these three
midpoints as the pedal point P2 is animated around the circumcircle. Second,
construct a circle with center at the circumcenter of triangle ABC such that
the radius is larger than the
radius of the circumcircle. Locate another pedal point (P1) on this circle and
trace the locus of the midpoints of the sides of its pedal triangle as P1 is
animated around the circle. It is interesting to find that the paths formed by
the locus of the midpoints are ellipses.
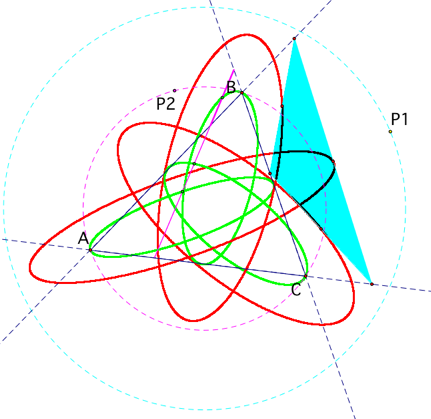
[The red paths are formed by the pedal point P1 and
the green paths are formed by the pedal point P2]
Click HERE if you want to play with these animations.