Bouncing Barney
By Pei-Chun Shih
Barney is in the triangular room shown here. He walks
from a point on BC parallel to AC. When he reaches AB, he turns and walks
parallel to BC. When he reaches AC, he turns and walks parallel to AB.
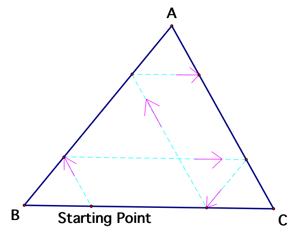
1.
Prove
that Barney will eventually return to his starting point.
2.
How
many times will Barney reach a wall before returning to his starting point?
3.
Explore
and discuss for various starting points on line BC, including points exterior
to segment BC.
4.
Discuss
and prove any mathematical conjectures you find in the situation.
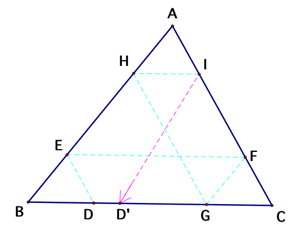
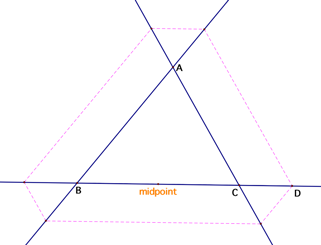
Assume that Barney starts at the point D and ends his
journey at point DŐ where D 
DŐ as shown above. Since BarneyŐs paths
are all parallel to the three sides of triangle ABC, the following are given:
DE || HG || AC, HI || EF || BC, and FG || DŐI || AB. Therefore, angle ABC = angle IDŐC because they are
corresponding angles of parallel lines AB and DŐI.
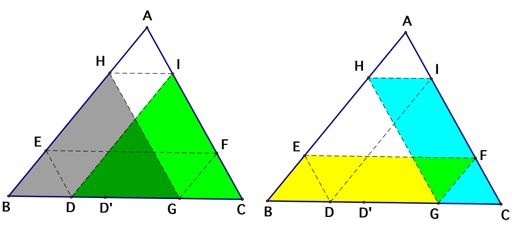
Next, letŐs connect the starting point, D, with point
I as shown below. We want to prove that triangle HBG is congruent to triangle
IDC that are colored with gray and green respectively. As we can see from the
triangle ABC on the right below, there are three parallelograms, BEFG, DEFC,
and GHIC, since their opposite sides are parallel as mentioned earlier.
Therefore, BG = EF = DC and HG = IC by the property of a parallelogram that the
opposite sides are equal in length.
Besides, the two angles BGH and DCI are equal since they are
corresponding angles of the parallel lines HG and AC. Hence, triangle HBG and
IDC are congruent by the Side-Angle-Side Congruence Axiom. So angle HBG = angle ABC = angle IDC.
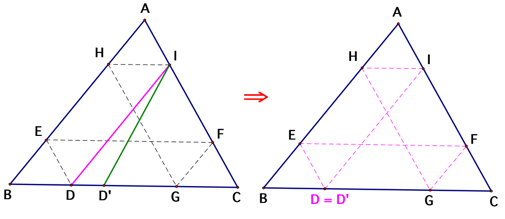
However, weŐve got the relation that angle ABC = angle
IDŐC from the fist section of our proof. Therefore, angle IDŐC must equal angle
IDC since both of these two angles are equal angle ABC. Thus, angle DIDŐ = 0
and line segments ID and IDŐ are congruent. We have proved that Barney will
eventually return to his starting point, D, since D = DŐ.
Now we know that Barney will eventually return to his
starting point, D. Here I am going to use another point of view to verify this
conclusion.
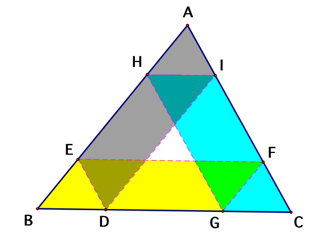
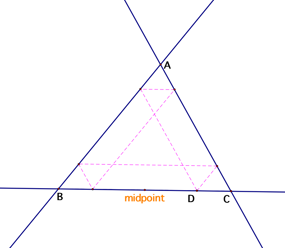
There
are several parallelograms inside triangle ABC as shown above since BarneyŐs
paths are always parallel to the three sides of triangle ABC. These parallelograms are BEFG, GHIC,
and AEDI as marked in yellow, blue, and gray respectively. By the property of a
parallelogram, the opposite sides are equal in length. Therefore, BG = EF, BE =
FG, CI = GH, CG = HI, AE = ID, and AI = DE. The total path of BarneyŐs journey
is the sum of the following segments: DE + EF + FG + GH + HI + ID which equal
AI + BG + BE + CI + CG + AE. After rearranging it, we get (AI + CI) + (BG + CG)
+ (BE + AE) = AC + BC + AB, which equals the sum of the three sides of triangle
ABC. Since the total paths of BarneyŐs journey are equal to the perimeter of
triangle ABC, we can view BarneyŐs traveling paths as he starts from point D
and goes along the perimeter of triangle ABC then back to the original point D
in the end. This is another way to verify that Barney will eventually return to
the starting point.
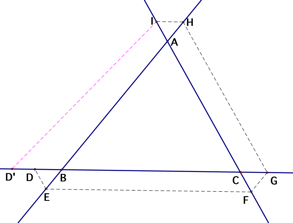
Now,
letŐs extend our discussions to the situation which the starting point is
outside triangle ABC. Suppose that Barney starts his journey at point D where
exterior to segment BC and follows the same pattern as he did earlier. Will he
return to his starting point as before? Assume that Barney ends his journey at point DŐ
where D DŐ as shown below left. Since BarneyŐs
paths are always parallel to the three sides of triangle ABC, the following are
given: DE || AC || HG, HI || BC || EF, and FG || AB || DŐI. Therefore, angle ABC = angle IDŐC because they are
corresponding angles of parallel lines AB and DŐI.
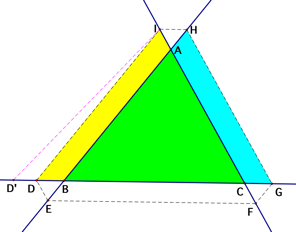
Next, letŐs connect the starting point, D, with point
I as shown above right. We want to prove that triangle HBG is congruent to
triangle IDC that are colored with blue and yellow respectively. As we can see
from the diagram above right, there are three parallelograms, BEFG, DEFC, and
GHIC, since their opposite sides are parallel as mentioned earlier. Therefore,
BG = EF = DC and HG = IC by the property of a parallelogram that the opposite
sides are equal in length.
Besides, the two angles BGH and DCI are equal since they are corresponding
angles of the parallel lines HG and AC. Hence, triangle HBG and IDC are
congruent by the Side-Angle-Side Congruence Axiom. So angle HBG = angle ABC = angle IDC.
However, weŐve got the relation that angle ABC = angle
IDŐC earlier. Therefore, angle IDŐC must equal angle IDC since both of these two
angles are equal angle ABC. Thus, angle DIDŐ = 0 and line segments ID and IDŐ
are congruent. Again, as we have proved before, Barney will eventually return
to his starting point, D no matter his starting point is inside or outside
triangle ABC.
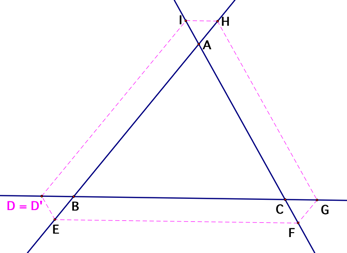
How many times will Barney reach a wall before
returning to his starting point? Well, it depends on where his starting point
is.
Suppose that his starting point D is always on the
line BC. If point D locates outside triangle ABC, then he will always reach a
wall five times
before returning to his starting point.
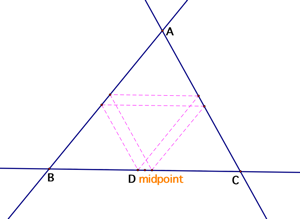
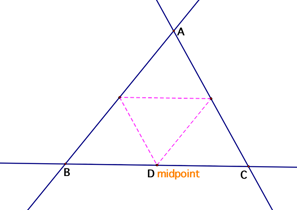
If D is any point inside triangle ABC except the midpoint of BC, then he
also needs to reach a wall five times before returning to D. However, if point D is the
midpoint of BC, then he will reach a wall only two times before returning to D.
