
Ceva’s Theorem
By Pei-Chun Shih
Consider any triangle ABC. Select a point P inside the
triangle and draw lines AP, BP, and CP extended to their intersections with the
opposite sides in points D, E, and F respectively.
Ceva’s Theorem says that in a triangle ABC,
three lines AD, BE, and CF are concurrent at a single point P if and only if ![]() .
.
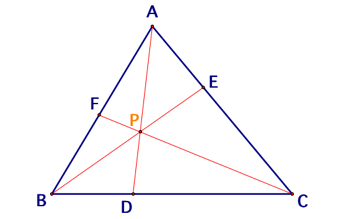
First, let’s explore (AF)(BD)(EC) and (FB)(DC)(EA) for
various triangles and various locations of P inside triangle ABC.
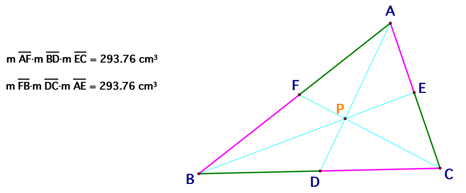
After exploring various triangles and various
locations of P via GSP, I found that the products of (AF)(BD)(EC) and
(FB)(DC)(EA) are always the same no matter what kind of triangle it is and no
matter where the location of P is as long as P is inside triangle ABC.
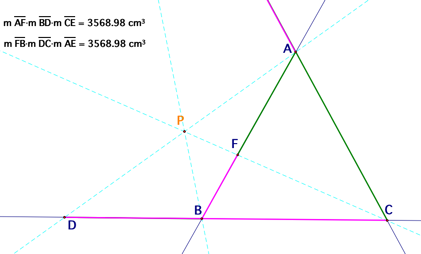
Next, I moved point P outside triangle ABC and found
that the products of (AF)(BD)(EC) and (FB)(DC)(EA) are still the same with
various triangles.
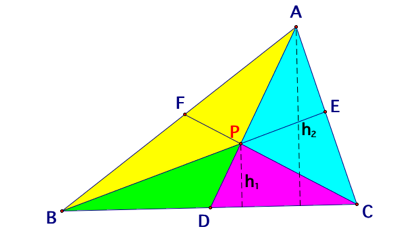
Here
I am going to prove the relationship discovered in the previous section by considering
areas of triangles inside triangle ABC.

After proving the Ceva’s Theorem, it is time to apply
it to the concurrency problems we have explored in the previous write-ups.
Recall that in the write-up 04, we proved the altitudes of a triangle are
concurrent by constructing circles and using the arc angle theorem. This proof
would be much easier by applying the Ceva’s theorem.
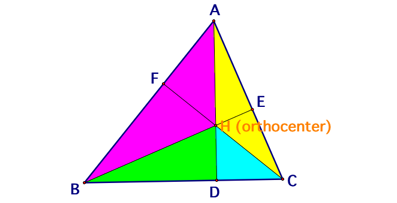
The diagram above shows triangle ABC with its
orthocenter H. Therefore, AD, BE, and CF are altitudes of triangle ABC. The
same technique we use to prove the Ceva’s theorem can be used here to prove
that the three altitudes are concurrent. Our goal is to find that the ratio of
(AF)(BD)(EC) and (FB)(DC)(EA) is equal to 1.

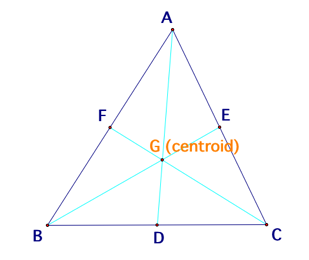
Proving the concurrency of three medians of a triangle
is a breeze if we use the Ceva’s Theorem. Below is the diagram of the centroid
of a triangle ABC. The points D, E, and F are the midpoints of triangle ABC
since AD, BE, and CF are medians. Therefore, BD = DC, EA = EC, and AF = FB. The
ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is equal to 1 since (AF)(BD)(EC) =
(FB)(DC)(EA). Thus, the three medians of triangle ABC are concurrent at G (the
centroid) by the Ceva’s theorem.
The proofs of the concurrency of the three angle
bisectors (if P is the incenter) or the three perpendicular bisectors (if P is
the circumcenter) of a triangle ABC are similar to the proof of the orthocenter
we have done earlier. Therefore, I would like to skip them here.
Basically the Ceva’s theorem is widely used in geometry
to prove the concurrency of lines in a triangle.