The Exploration of the Sine Function

Y=a sin(bx+c)

I will explore the function y=a sin(bx+c) for different values of a, b, and c. Let’s first start with the graph of the basic sine function, where a=1, b=1 and c=0. All other variations will be compared to this function.

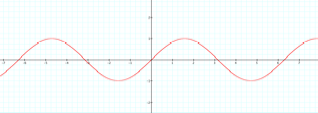
The domain of f(x) is the set of all real numbers. The range is the interval [-1,1]. The function has a period equal to 2pi, and an amplitude, which is the maximum value of f(x), of 1.

Now let’s vary the value of b, while a and c remain constant.

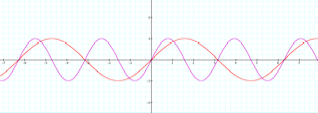
The value of b changes the period of the graph. The period is the horizontal distance along the x-axis between two points, one is the starting point of a cycle and the second point is the end point of the same cycle. As |b| increases, the graph of f(x) is compressed. Let’s see what happens if |b| decreases.

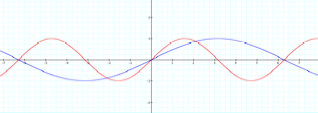
As |b| decreases, the graph of f(x) is stretched. Furthermore, the period of each function is equal to |(2pi/b)|. Now, let’s see what happens if b is negative.

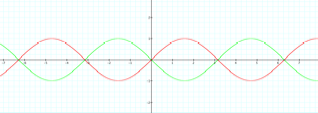
And what about if a is negative?

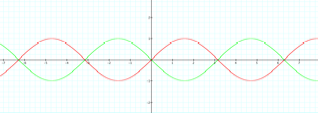
Notice that sin(-x) and –sin (x) yields the same graph. The negative values for a and b reflect the function about the x axis.

Now let’s vary the value of a, while b and c remain constant.

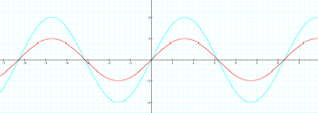
As |a| changes, the amplitude, which is the maximum value of f(x), changes. In fact this maximum value is equal to |a|.

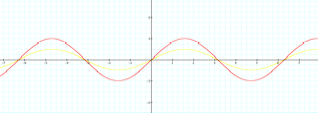
As |a| decreases the maximum value of f(x) decreases.

Now let’s vary the value of c, while a and b remain constant.

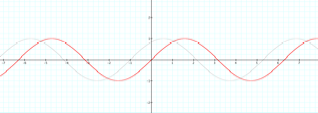
A positive c value causes a shift of the graph of f(x) to the left. This phase shift is equal to –c/b. Now let’s see what will happen with a negative c value.

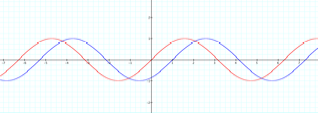
A negative c value causes a shift of the graph of f(x) to the right.

In conclusion, a modifies the amplitude, b modifies the period and c modifies the phase shift of a sine function.