Polar Equations

I will investigate the polar equation, , for different values of a, b, and k.

Let’s start by graphing this polar equation when a, b, and k are all equal to 1.

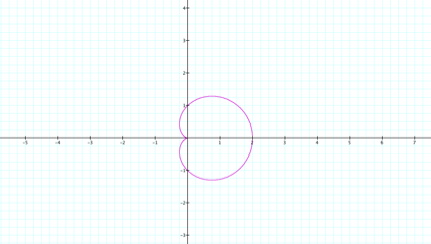
Now let’s keep a and b equal to 1 and change the value of k to 2.

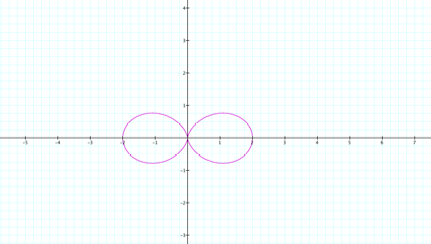
It looks like there are two leaves on the graph. These leaves cross the x axis at the origin and at 2 and -2.

Now, let’s keep a and b equal to 1, but change k to a value of 3.

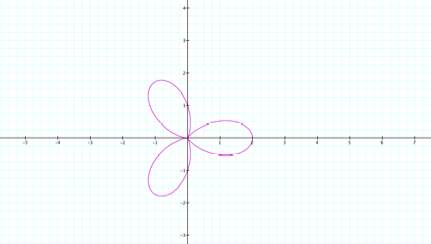
Notice, now there are three leaves and they all intersect at the origin.

Now, let’s try a larger value for k and see what happens. Let’s try k=15.

Now, I have 15 leaves. It looks like k changes the number of leaves.

Now, let’s try k=100.

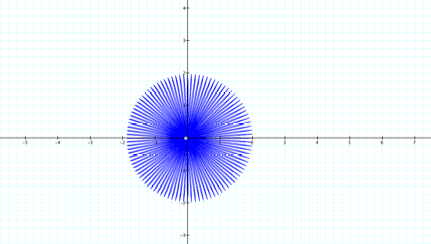
Wow, look at that, it almost resembles a flower.

So, when a and b are equal, and k is an integer, the function forms an “n-leaf rose”.

Now, let’s look at the function , when k=0 and b=1.

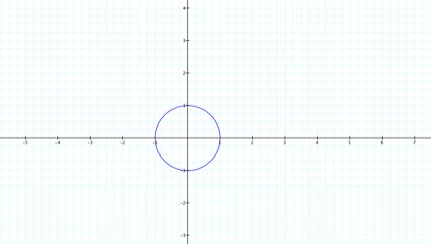
This is the graph of the cosine function on the polar coordinate map. There is only one leaf.

Now, let’s try k=2 and let b remain 1.

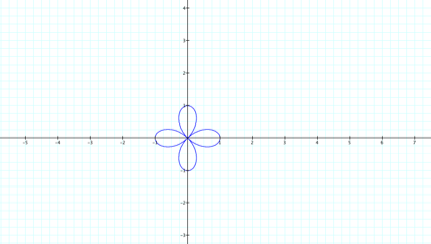
The graph now has 4 leaves. Maybe the number of leaves is now 2k. Let’s see.

Let’s try k=3 to see if we get 6 leaves.

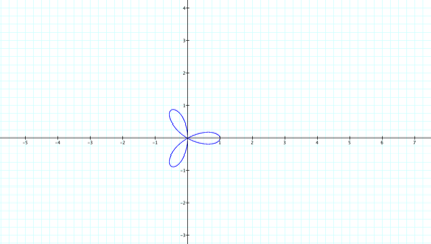
Intersecting, I only get 3 leaves. So the above conjecture is not correct. Let's try k=4.

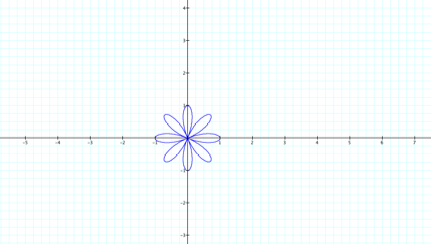
Well, now I have 8 leaves. Maybe the leaves being equal to 2k only works when k is even. Let's try when k= 6.

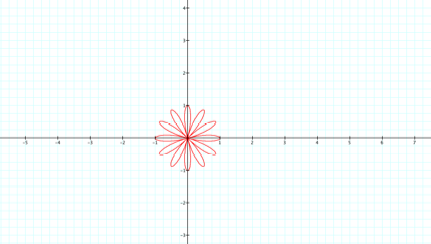
Yes, my above conjecture seems to be correct. When k is odd the number of leaves is k. But when k is even the number of leaves is equal to 2k. Let's try one more odd value just to be sure. Let’s try k=9.

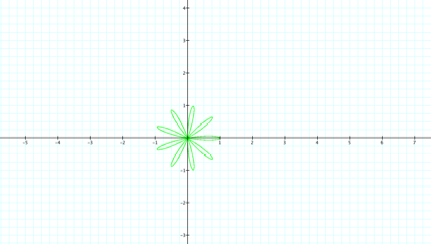
Yes, there are only 9 leaves, I was correct.

Now, lets change the value of b, while k remains constant. Let b=2 and k=2.

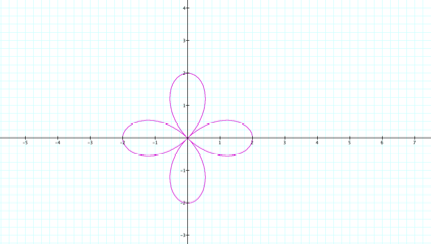
Let’s try a few more before I make a conjecture.

What about when b= 3 and b=6.

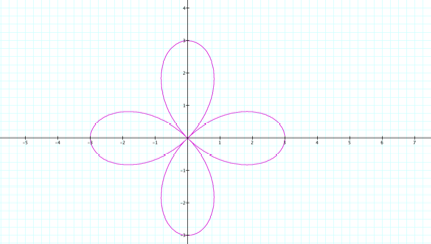
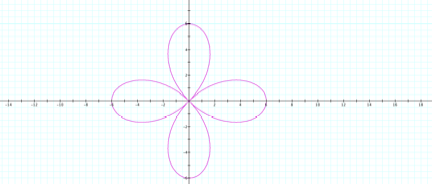
It appears that the value of b effects where the function intersect both axis. For instance, when b = 6, illustrated above, the function intersects the x and y axis at 6 and -6 .

Now, let’s see what happens if I graph the function , and how this compares with the graphs of .

Let’s see what happens when k=0 and b=1. This yield no graph at all. Let’s change k to 1.

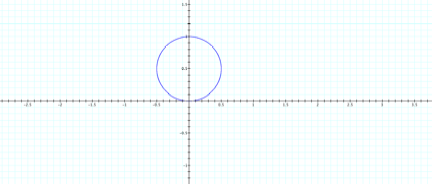
This graph has only one leaf.

Let’s see what happens when k=2.

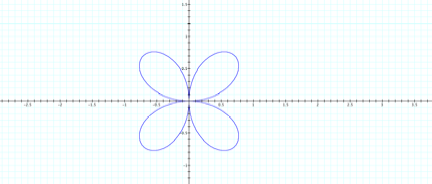
This looks like this might follow the same pattern as the cos function.

Let’s try another even value and then a couple of odd values for k.

First, let’s try k=4. Will there be 8 leaves?

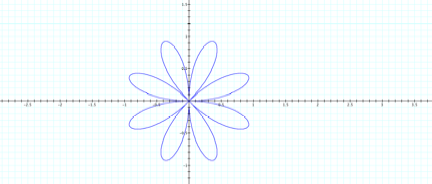
Yes, so the k must determine the number of leaves as before. So, there will be 2k leaves.

Now, what about the odd values, let’s try k=5. Will there now be 5 leaves?

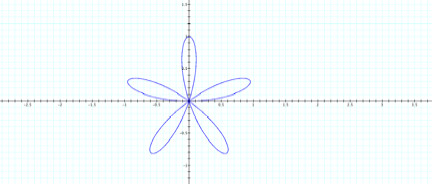
Yes, let’s try one more, k=11.

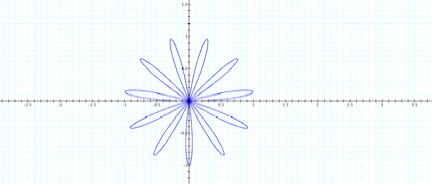
So, there are 11 leaves. It looks like the graph of the cosine polar function is the same as the graph of the sine polar function. But, I have to try one more case. What happens when the value of b is altered and k remains constant. Let’s try b=2 and k=2.

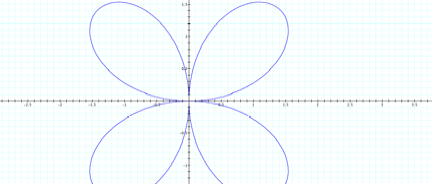
I see that the b value does expand the function. But there seems to be a rotational shift. Let’s try one more

b= 4 and k=2.

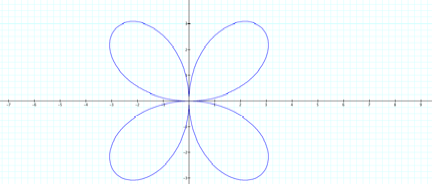
Yes, the graph is a definite rotation from the cosine function. It looks to be a 90 degree rotation.