Proof that the Altitudes of a Triangle are Concurrent

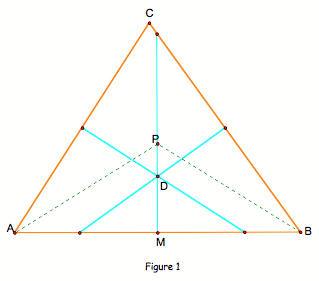
Proof: To prove this, I must first prove that the three perpendicular bisectors of a triangle are concurrent. From Figure 1, consider triangle ABC, I know that the perpendicular bisector of AB, passing through midpoint M of AB, is the set of all points that have equal distances to A and B. Let’s prove this: Consider P, a point on the perpendicular bisector. Because, PM is congruent to PM, MA is congruent to MB and <PMA is congruent to <PMB, I know that triangle PMB is congruent to triangle PMA by SAS. And I can conclude that all of the points on the perpendicular bisector are equal distances from A and B. So, we know that the perpendicular bisectors of AB is the set of all points P such that PA is congruent to PB and this relation is true for all sides of the triangle. Consider D, which is the intersection of the perpendicular bisectors, then I know that DA is congruent to DB which is congruent to DC. So, D lies on the perpendicular bisector of BC and AC also, thus the three perpendicular bisectors of a triangle are concurrent.

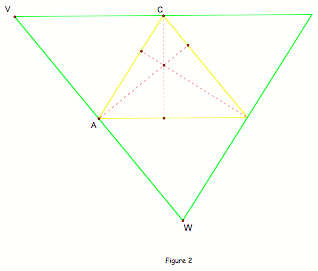
In Figure 2, consider triangle ABC, consider a line through A parallel to BC, through B parallel to AC, and through C parallel to AB. This forms a new triangle UVW. From this construction, consider parallelograms VCAB, CUAB and ACWB. Because opposite sides of a parallelogram are congruent, AB is congruent to VC and AB is congruent to CU, therefore VC is congruent to CU, so C is the midpoint of VU and similarly A is the midpoint of VW and B is the midpoint of UW. Now consider the perpendicular bisector of UV, it passes through C, it is perpendicular to UV. But if it is perpendicular to UV, it is also perpendicular to AB, because AB and UV are parallel. So the perpendicular bisector of UV is the altitude from C in triangle ABC. I can conclude that the perpendicular bisectors of UVW are the altitudes in ABC. Since I have proven that the perpendicular bisectors of UVW are concurrent, the same is true for the altitudes in ABC. QED