Exploration of Three Points

Given points A, B, and C. Draw a line intersecting AC in the point X and BC in the point Y such that AX=XY=YB.

Let’s construct the given three points and angle ACB.

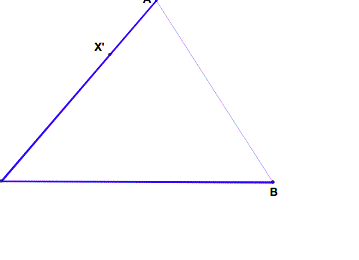
My first step is to construct the segment AB. Here, I will draw it with a dotted line because it is only for construction purposes. Also, I will identify an arbitrary point, let’s call it X`, on segment AC.

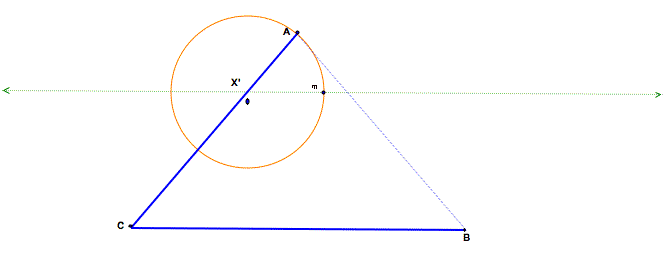
Now I will construct a circle about the point X`, with a radius the length of segment X`A. Then I can construct a line parallel to segment CB passing through X`. Now I will mark the point in the interior of angle ACB, which is the intersection of our circle center at X` and the parallel line passing through X`. Let’s call this point m.

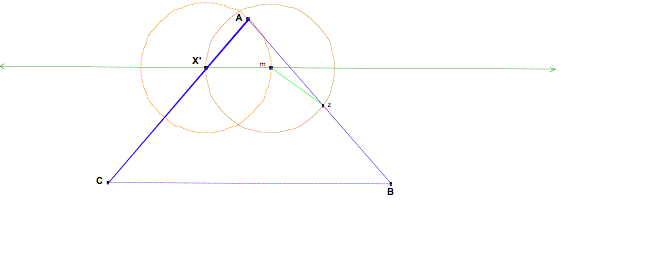
Now, I want to find a point, let’s call it z, on segment AB such that X`m = mz. To do this we construct a circle about point m with radius equal to the length of X`m. Then I will construct the intersection of the circle and segment AB.

Now I have three point X`, m and z and two segments X`m and mz which are equal in length. Thus, I can construct a rhombus by finding the fourth point, let’s call it Y`, such that X`m=mz=zY`=Y`Z`. To do this, I can construct the line passing through point X’ that is parallel to mz. The intersection of this parallel line and our circle about point X`, which is the interior of angle ACB, is our point Y`. Now I have a rhombus.

Using my rhombus, I can determine the location of point Y. First I construct the ray AY`. The intersection of ray AY` and segment CB is point Y. This is the projection of Y` onto segment CB.

I now need to find X. To find X, I need to construct a circle about point A with a radius equal to the length of segment YB. The point where the circle intersects segment AC is point X.

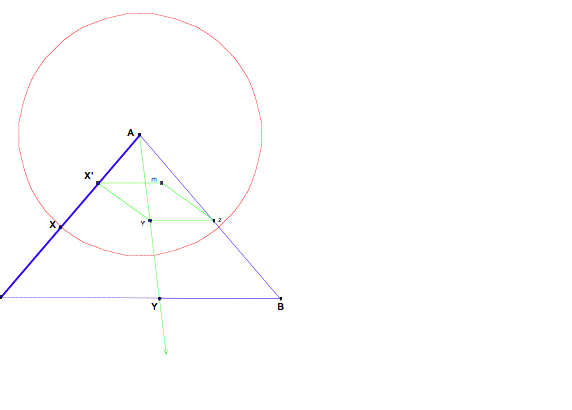
Finally I have point A,B,X and Y such that AX=XY=YB. The following illustration show circle about points X and Y with radius equal to the length of XY.