Altitudes and Orthocenters

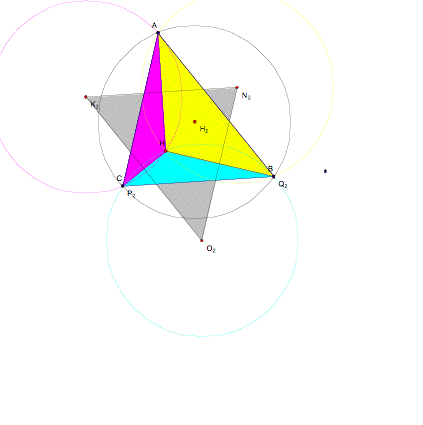
Let’s first construct a triangle ABC, with orthocenter H.

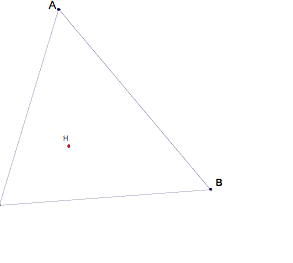
Now, let’s construct three more triangles from the orthocenter to the vertices of the larger triangle.

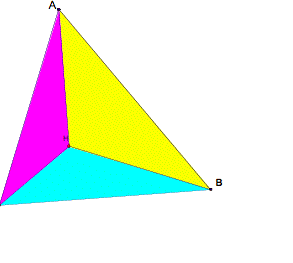
Now, let’s construct the orthocenters of triangle ACH, triangle ABH and triangle BCH.

Notice that the orthocenter of triangle ACH is point B, the orthocenter of triangle ABH is point C, and the orthocenter of triangle BCH is point A.

Now, let’s construct the circumcircle of all four triangles: triangle ABC, triangle ACH, triangle ABH and triangle BCH.

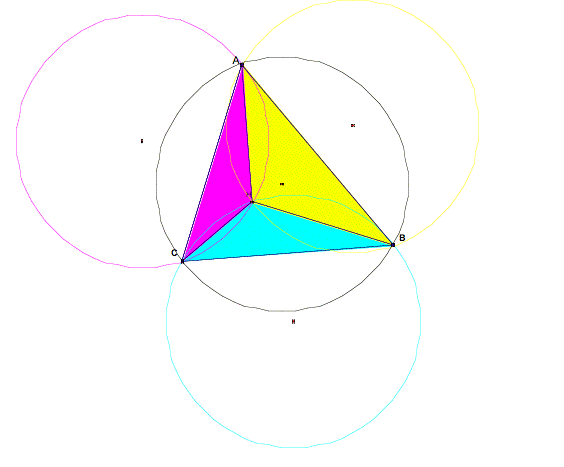
It appears as if the four circumcircles are congruent, let’s find out.

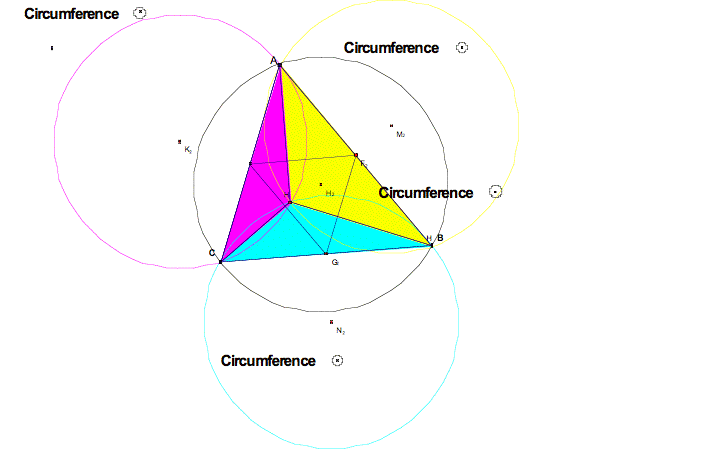
Yes, using GSP measurement tools, I know that the circumcircles are congruent. Now let’s see what will happen if I created a triangle using the centers of the colored circumcircles as vertices.

Wow, this triangle is congruent to our original triangle ABC.

Conjectures:

Given a triangle ABC and its orthocenter H, we can construct three triangles, triangle ACH, triangle ABH and triangle BCH such that:

1. The circumcircles of all four triangles are congruent.

2. The intersection of any two of the circumcircles belonging to the smaller triangles is a vertex of the given triangle ABC.

3. The orthocenters of the smaller triangles is a vertex of the larger triangle.

4. A triangle formed by connecting the centers of the circumcircles of the smaller triangles is congruent to the original triangle ABC.