Bouncing Barney

Given triangle ABC, Barney is standing against one wall in a triangular room.

Barney walks to a 2^nd wall (wall AB) by moving parallel to the third wall(wall AC).

Once Barney gets to this wall he turns and walks to the third wall AC by moving parallel to wall BC. This process continues as Barney walks from one wall to the next by moving parallel to the third wall.

Do you think that Barney will return to his starting point? If so, how many times will he intersect each side?

What if Barney starts from another point on BC, will the result remain true? Let’s see.

Yes, Barney seems to always return to his starting point and crosses each side twice in the process. Now let’s investigate some findings when Barney starts at various points.

Here Barney starts at the midpoint of BC. Notice, that Barney still returns to the starting point, but only intersects each side of the triangle once. Also, it appears that Barney also intersects the other two sides at their midpoint. Additionally, it appears that Barney’s path divides triangle ABC into 4 congruent triangles. Let’s see if this is true.

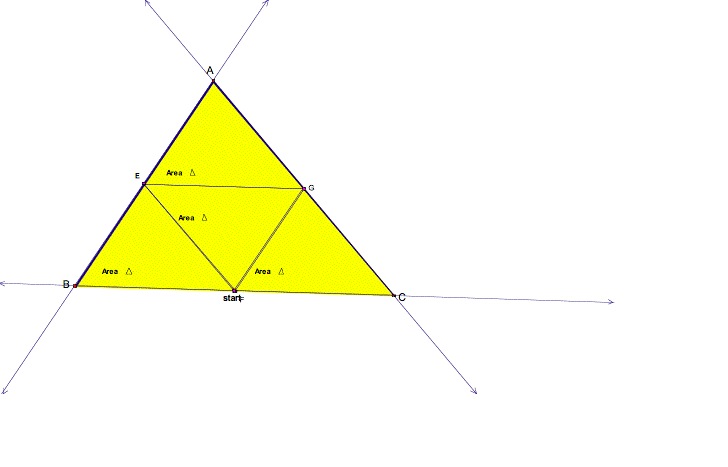
Yes, it appears that my conjecture may be correct. But remember that GSP measurements are not proofs.

What if the starting point was one third the distance of BC, does anything noteworthy happen?

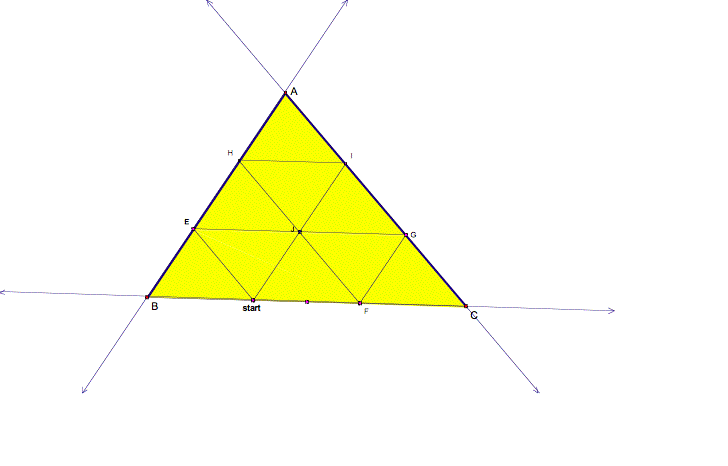
It appears that the paths create 9 congruent triangles, let’s measure to see if my conjecture is correct.

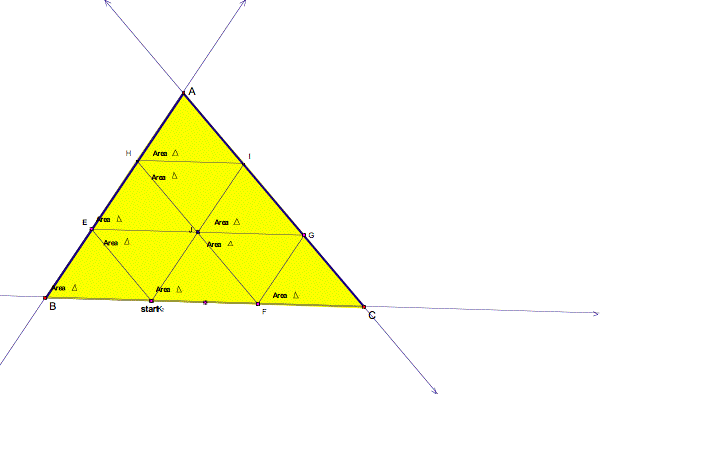
Yes, the path creates 9 triangles of equal perimeter and area and also trisects each side of the triangle. Lastly, what if the starting point was one fourth the distance of BC?

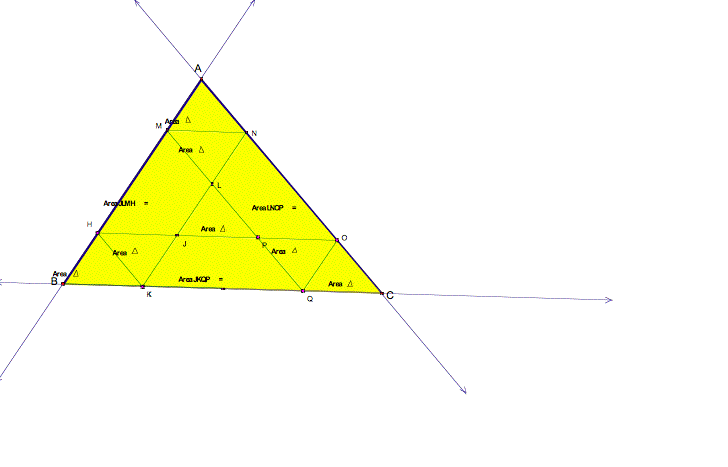
This is very intersecting, the path divides the triangle into 3 congruent trapezoids and 7 congruent triangles.

As I explore the different starting points of Barney, I notice that when Barney starts inside the triangle (or on one of the vertices), the distance he travels to reach his starting point is equal to the perimeter of the original triangle. Let’s prove that here:

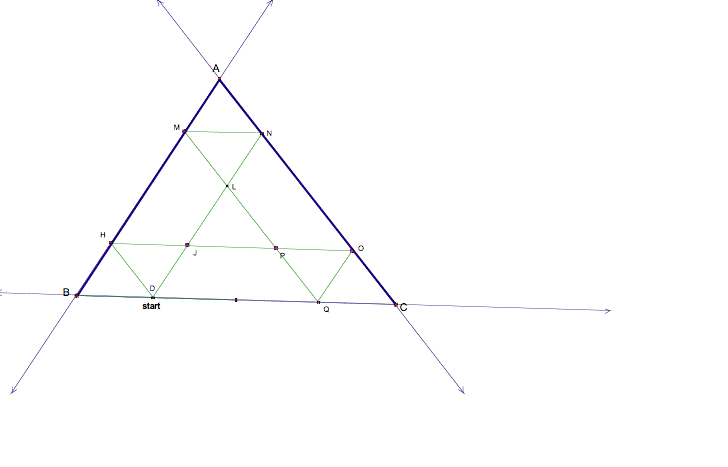
Let the starting point be D and H, M, N, O and Q represent the points where Barney reaches the different sides of the triangle. So, the segment paths that Barney travels are DH, HO, OQ, OM, MN, and MD, in that order. Let J, L and P be the intersections of Barney’s travel.

I know that AB = BM+MA. Since BMHD is a parallelogram, BM=HD and since MAOQ is a parallelogram, MA=OQ. So, by substitution, AB=HD + OQ.

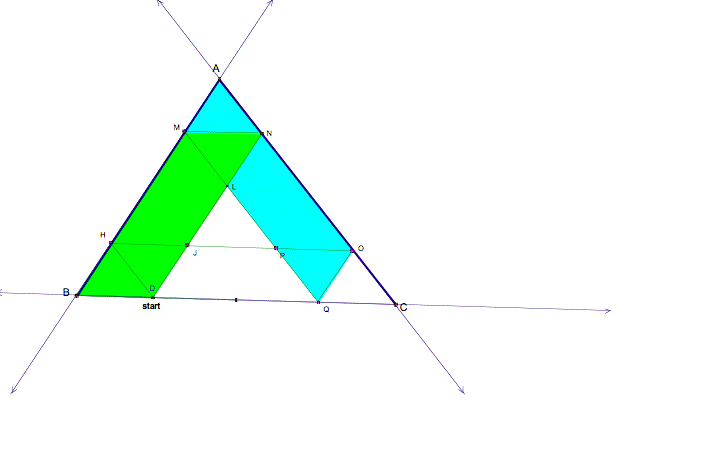
Similarly, I know that AC= AN+NC. Since ANDH is a parallelogram, AN=DH and since NCQM is a parallelogram, NC=QM. So, AC= DH + QM.

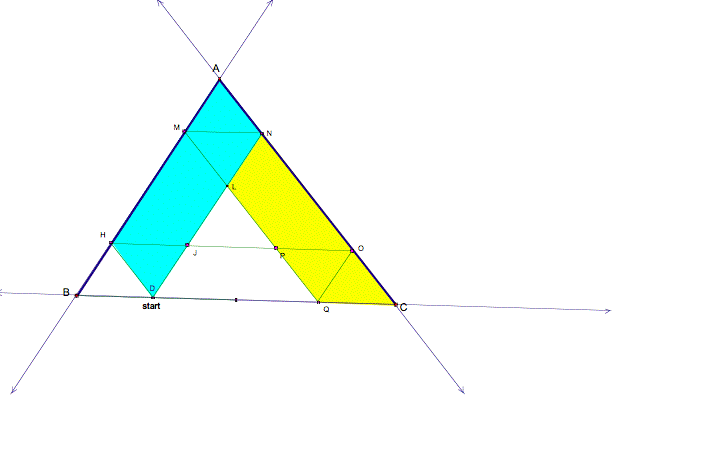
And finally, I know that BC = BQ+ QC. Since BQOH is a parallelogram, BQ=OH and since QCNM is a parallelogram, QC=MN. So, BC=OH+MN.

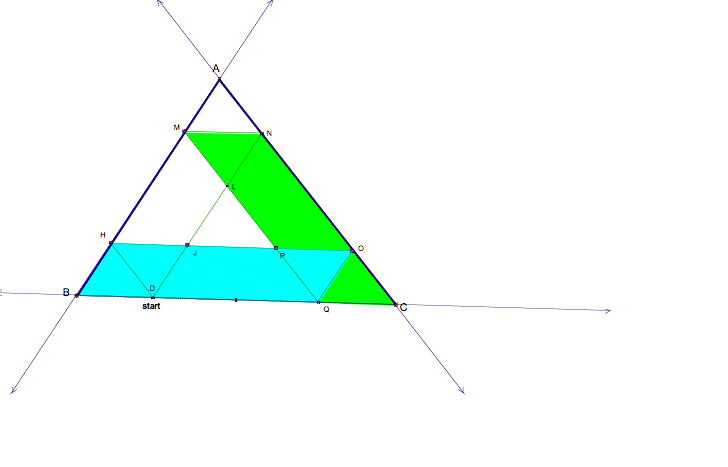
Therefore, AB+BC+AC= HD + OQ+ DH + QM+ OH+MN.

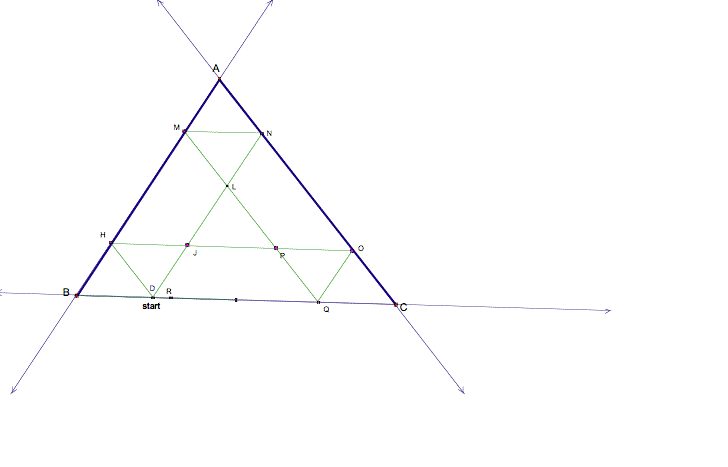
Another exception to this proof, is when the starting point is the midpoint of a side, in which case the sum of the paths is half of the perimeter of the triangle.

What happens if Barney starts on a point outside of the triangle? Let’s see:

The path encompasses the triangle, but it does return to the starting point. By using directed measuresments, it can be determined that the path of Barney outside of the triangle, is also the perimeter of the original triangle.