Ceva’s Theorem

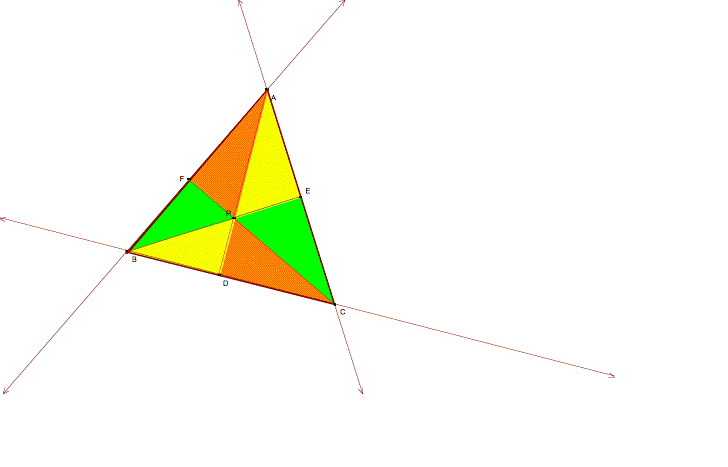
I will start my investigation by considering a triangle ABC and an arbitrary point P inside the triangle. We will construct line AP, BP, and CP and extend those lines to intersect the opposite sides at points D, E, and F respectively. I will explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and locations of P.

Consider the above construction. The strategy will be to construct a line through P which is parallel to each of the three sides of ABC. Doing this will allow me to locate similar triangles and this will help me to relate their sides.

By constructing a line through P and parallel to AB, I can determine congruent angles which leads to similar triangles.

By the corresponding angle theorem, angle AFC is congruent to angle HPC and angle FAC is congruent to angle PHC. This implies that triangles AFC and HPC are similar or AF/HP=FC/PC, by AA Similarity Theorem.

By the same argument I can say that triangles BFC and JPC are similar or BF/JP=FC/PC. By the above I could also write AF/BF = HP/JP.

I can also see that triangles BAE and HPE are similar, then HP/AB = PE/BE.

Furthermore, I see that triangle BAD is similar to triangle JPD, then JP/BA=PD/AD.

So, AF/BF = HP/JP = (HP/AB)/(JP/AB) = (PE/BE)/(PD/AD).

Now, let’s construct another parallel line through P parallel to BC.

As I did before, I will locate similar triangles.

Triangle ABD is similar to triangle AIP and PAK is similar to DAC resulting in BD/IP = AD/AP and DC/PK = AD/AP. This, then implies BD/DC = IP/PK and PE/BE = PK/BC giving me FP/FC = IP/BC.

Therefore, BD/DC = (PJ/BC)/(PK/BC) = (FP/FC)/(PE/BE).

Finally, let’s consider a line through P parallel to AC.

Now, let’s locate similar triangles.

Triangle BEC is similar to triangle BPM, so EC/PM = BE/BP.

Triangle ABE is similar to triangle LBP, so AE/LP = BE/BP which implies that EC/PM = AE/LP.

Triangle CDA similar to triangle DPM, so PM/AC = PD/AD.

Triangle AFC is similar to triangle FLP, so LP/AC = FP/FC which implies that EC/AE = PM/LP = (PM/AC)/(LP/AC)=(PD/AD)/(FP/FC)

At last, let’s put this all together.

(AF/FB)*(BD/DC)*(EC/EA) = (PE/BE)/(PD/AD) * (FP/FC)/ (PE/BE) *(PD/AD)/(FP/FC) = 1

So this proves that (AF/FB)*(BD/DC)*(EC/EA) = 1.

Next, let’s use Ceva’s Theorem to show the concurrency of altitudes of a triangle.

I know that AD is the altitude of BC, BE is the altitude of AC, and CF is the altitude of AB.

By the Angle-Angle Similarity Theorem, I know that triangle AFD is similar to triangle CDP, triangle BFP is similar to CEP and triangle BDP is similar to triangle AEP.

Thus, (AF/CD)=(AP/CP)=(FP/DP) , (BF/CE) = (BP/CP) = (FP/EP) and (BD/AE)=(BP/AP)=(DP/EP).

Which implies that (CP)(FP)=(AP)(DP), (CP)(FP)=(BP)(EP), and (BP)(EP)=(AP)(DP).

So, (AP/CP)=(FP/DP)=(BP/CP)=(FP/EP)=(BP/AP)=(DP)(EP), therefore (AF/CD)=(BF/CE)=(BD/AE).

Finally, I can conclude that (CD/BD)*(BF/AF)*(AE/CE)=1.

Therefore the converse of Ceva’s Theorem confirms that the altitudes are concurrent.

Next, let’s use Ceva’s Theorem to show the concurrency of angle bisectors of a triangle.

Considering the following figure, AD is the angle bisector of angle A, FC is the angle bisector of angle C, and BE is the angle bisector of angle B. By the Angle Bisector Theorem I know that (BD/CD) = (AB/AC) and similarly (AE/CE) = (AB/BC) and (AF/BF) = (AC/BC).

This implies that AB = ((BD)(AC))/CD and that AB = ((AE)(BC))/CE.

So, by substitution, I know that ((BD)(AC))/CD = ((AE)(BC))/CE

Cross multiplication gives us (BD)(AC)(CE)=(CD)(AE)(BC) which is ((BD)(AC)(CE))/((CD)(AE)(BC)) = 1.

From above, I also know that AC = ((AF)(BC))/BF. Now by substituting AC = ((AF)(BC))/BF into ((BD)(AC)(CE))/((CD)(AE)(BC)) = 1, I receive ((BD)(CE)(AF))/(CD)(AE)(BF)) = 1. So Ceva’s Theorem confirms the concurrency of angle bisectors.

Now let’s use Ceva’s Theorem to show the concurrency of medians of a triangle.

Consider the following construction, AD bisects BC, BE bisects AC and CF bisects AB.

Since AF=BF, BD=CD and AE=CE, I can say that (AF/BF)=(BD/CD)=(AE/CE)=1, so ((AF)(BD)(CE))/((BF)(CD)(AE))=1. Therefore, Ceva’s Theorem confirms that the altitudes of a triangle are concurrent.

Lastly, what happens when P is outside of the triangle? After viewing a GSP sketch it appears that Ceva’s Theorem still holds when P is outside the triangle.

Click here for a GSP file to further explore this case.