
Hillary Tidd
Transformational Geometry: Tessellations
Once students have had the opportunity to explore the various properties of angles and triangles, they can apply their knowledge to look deeper into Transformational Geometry and more specifically, Tessellations. In this unit we will explore properties of how different geometric figures move through translation, rotation and reflection. Once we are familiar with the various movements we will create our own Tessellation.
First lets look at translations!
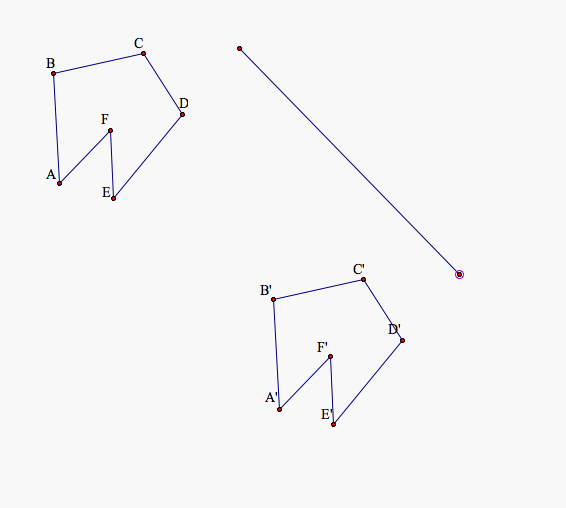
First we'll create a geometric figure to translate using Geometer's Sketch Pad. Translation essentially means to move from point A to point B. The diagonal line serves as our "line of translation," it tells us how far and in which direction we will move our figure. During this translation the figure stays in the same in the exact same position and it simply move along the line of translation. What are some observations you can make about the movement of this figure?
How about reflection?
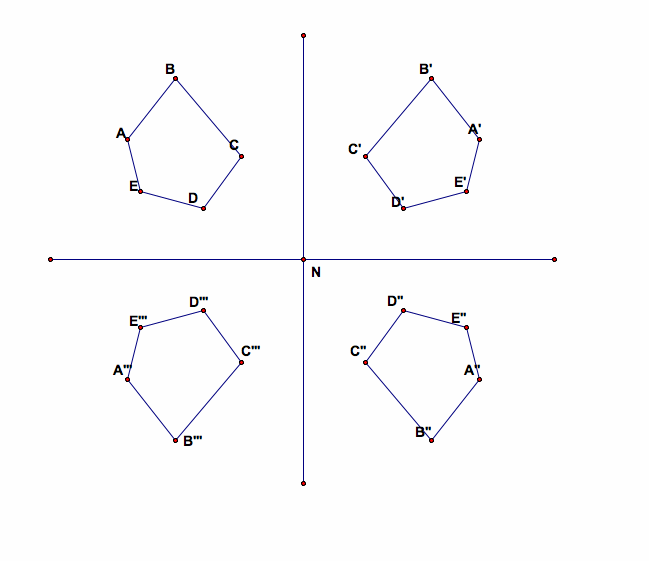
Next we'll create another figure to use in our exploration of reflection. Reflection symmetry is where a figure is reflected over a particular "line of reflection" and the reflected figure is a mirror image of the original. You know how you look in a mirror and the objects you see are backwards? That is exactly how reflection symmetry works. Figure ABCDE is looking in the mirror at figure A'B'C'D'E. In this particular figure, the geometric figure is reflected three times. What are some observations you can make about the movement of this figure?
What about Rotation?
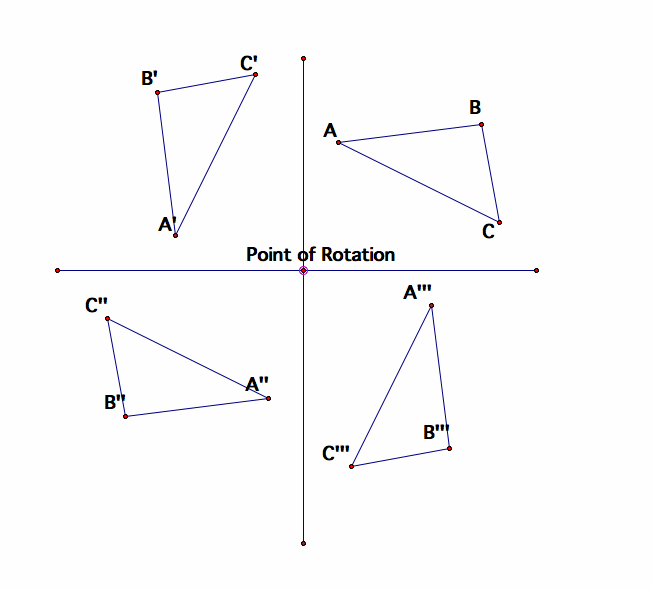
Now we've created a triangle to see what would happen to it if we rotated it. In this figure the point of rotation is labeled and that is the point about which the triangle will move. Think about it as a paper football on your desk. If you were to place your thumb in a set position on the desk and move the paper football with your index finger, you would be rotating the football about the fixed point of your thumb. In our image above, we have rotated the triangle four times to get it back to the original position. What observations can you make about rotating an object? If it make a complete rotation, how many degees did the triangle move?
But what is a Tessellation?!

A Tessellation is a collection of plane figures that fills the plane with no overlaps and no gaps. Artists and mathematicians use the geometry properties that we just learned to create very unique drawings. We are going to use our knowledge of geometry and Geometer's Sketch Pad to create our own tessellations.
Lets do a Tessellation!!

First we start with a basic rectangle shape. What are properties we know about rectangles? Measure the area of this rectangle.

Next we cut a particular shape off of one side of the rectangle and paste is to the opposite side. We do this in GSP by marking our vector as the length of the top of the rectangle in the direction we want the piece to move. Now what are some properties you can see of this shape? Measure the area of this new shape. Is it the same as the rectangle? If so, you're doing great so far!
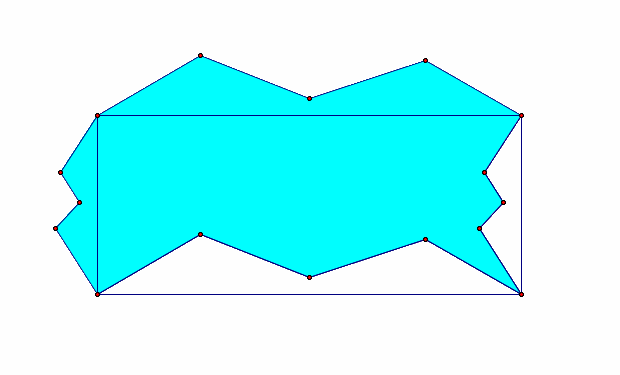
Now we'll do the same thing that we did to the sides to the top and bottom. We cut a particular shape from the bottom of our rectangle and placed it on the top. This time our vector is the side of the rectangle from bottom to top. You can see from our original rectangle lines still in the picture that our area should maintain the same. What are some properties of this shape that you can see? Measure the area. Is the the same as our original area?
Now what do we do with this shape? We're going to copy it as many times as possible and fit them all together like puzzle pieces!!

Making each shape a different color really helps to see how they fit together! This is an example of a Tessellation with just translational symmetry.
Let's try a Tessellation with rotation!!

With creating a rotation tessellation it would be best to start with a square as opposed to a rectangle we did before. What are the properties of squares? What is the area of our starting square?
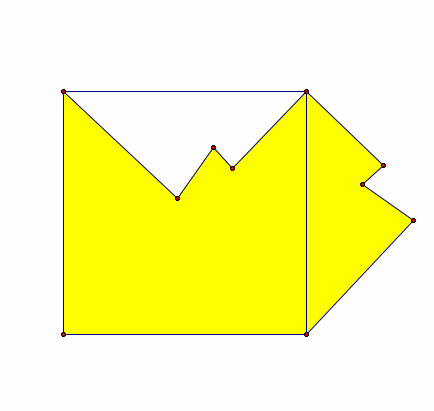
Next we're going to cut a shape from the top of our square and rotate it 90 degrees about the top-right point of the square and place it on the right side of the square. The top-right point is our fixed point to use as rotation. Now what are some observations you can make about this shape? Measure the area. What do you notice?
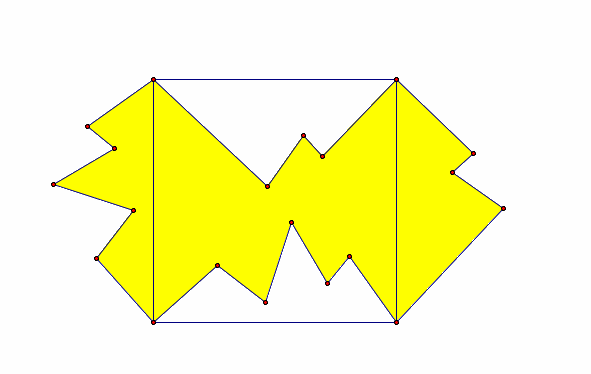
Here we did one more rotation, but this time the bottom-left point of the square was our fixed rotation point. What can we say about this shape? What does it look like? Measure the area. Is it the same as our original square? Good!
Now we'll fit our pieces together like a puzzle, but be careful. This one will be a little trickier to fit together!

Tessellations can be found everywhere!! Look at the tile floor in the hallways or even the brick walls of the school! Tessellations come in any shape and size, so be aware of all the geometry this is around you all the time!