Summer Tuggle
Assignment
1.2
Let’s
examine what happens when we combine two linear functions using basic
computations.
We
want to explore these 4 different cases
l. f(x) + g(x)
ii. f(x) * g(x)
iii. 
iv. f(g(x))
Let
f(x)= 
x+1 and g(x)= 3x-4
i.
What
happens when you add two linear functions?
What will the graph of the result look like? Is it linear? Explain why
or why not.
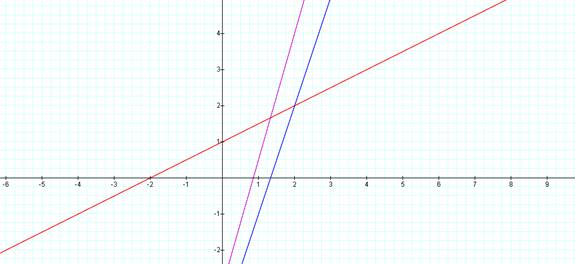
The red line
represents f(x) and the blue line represents g(x). The purple is represents the function created
by adding f(x) and g(x). It is still
linear because when you add variables you only add coefficients. The power on the variable will stay the same.
ii. What happens when you multiply two linear functions? Can you
use the laws of exponents to predict what your graph will look like?
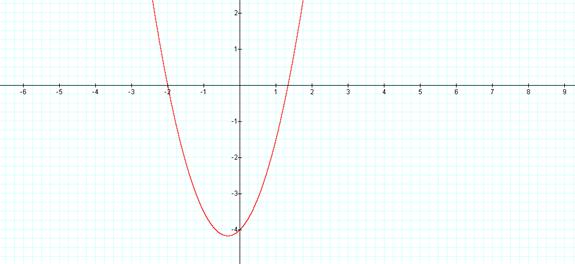
When you
multiply two linear functions you will create a quadratic function. The law of exponents states that when you
multiply variables, you add the powers.
Therefore the power on the x becomes 2.
iii. Now try
dividing the functions.
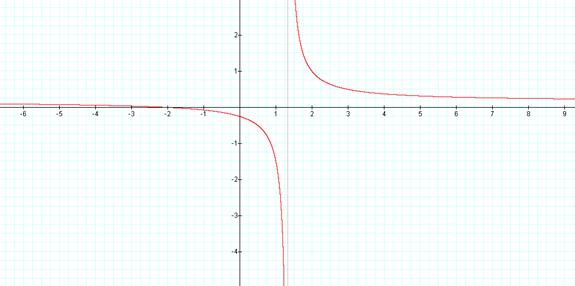
This graph is called a hyperbola. There is an interesting gray line on the
graph. Where does it occur (write the
equation for this gray line). What
significance does this line have? Why is
at this specific point? How do we find where the graph will cross the x and y
axis? How can you see these points in the equation?
The equation
for the gray line is x=
. This is the value
for x where the denominator will equal zero.
The function is undefined at this point.
Therefore the red lines will not cross this vertical line. This is
called the vertical asymptote. There is
also a horizontal asymptote. In order to
find the horizontal asymptote, you must first solve for x and then find where
the function will be undefined (the value of y that will make the denominator
0).
Y=
Therefore
the function will
Y(3x-4)=1/2x +1 be undefined
when
3xy-4y-1/2x+1 3y-1/2=0
3xy-1/2x=1+4y 3y=1/2
X(3y-1/2)=1+4y y=1/6
X=
The place
where the graph crosses the x- and y-axis are called the x-intercept and the
y-intercept. To find the x-intercept you
allow y to equal 0. In order to proceed,
you will be multiplying the denominator by 0 so you can just set the numerator
equal to 0 to solve for the x-intercept. Conversely allow x to equal 0 in order
to find the y-intercept. For this
equation h(x)=the x-intercept is (-2, 0) and the y-intercept is (0, -1/4). You can see these points easily in the
equation by setting the numerator equal to 0 (this will produce the
y-intercept) and by eliminating the expressions with the variable x (which will
provide the x-intercept).
iv. What does the graph of f(g(x)) look like? Is it linear? Why? How do we find this
function algebraically?
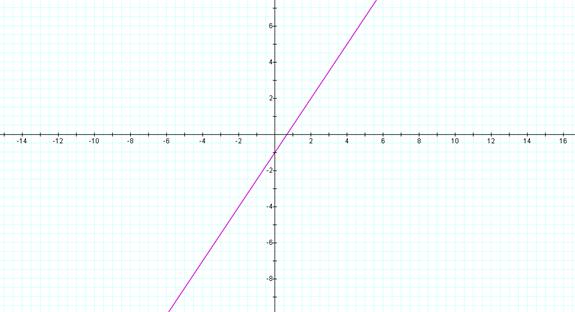In order
to find this function algebraically, you must replace the x in the f(x)
function with the equation for g(x). So f(g(x))=1/2(3x-4)+1
and once simplified it becomes (f(g(x))=3/2x-1.
The new equation is linear because you are merely replacing one x with
another value of x. The two x’s are not being multiplied
together so the power remains 1.