Summer Tuggle
Final
Assignment part I
Bouncing Barney
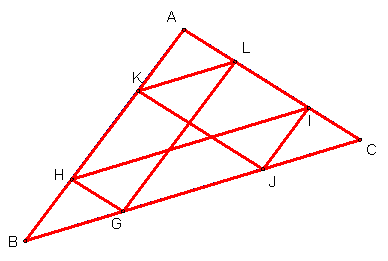
Barney is in the triangular room shown here. He walks from a point on BC
parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he
reaches AC, he turns and walks parallel to AB. Prove that Barney will
eventually return to his starting point.
Barney
starts at point G and walks to H, I, J,K, L and then
back to G following the rules stated in the problem.
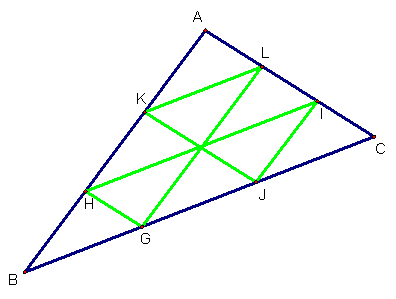
Using
Geometer’s Sketchpad, you can manipulate the construction to make all the
intersections concurrent with one of the vertices of triangle ABC.
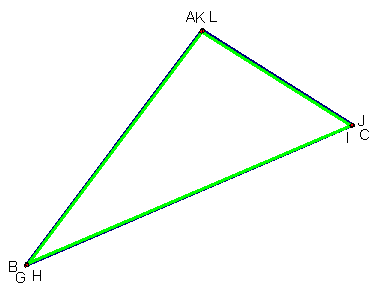
It
seems that Barney’s green path is the same as the perimeter of the original
triangle. If proven that the green path
is equal to the blue path, then we could assume that Barney will always end up
where he started. The next construction shows point G in a different spot than
in the first two pictures and again it seems that G is the beginning and ending
point.
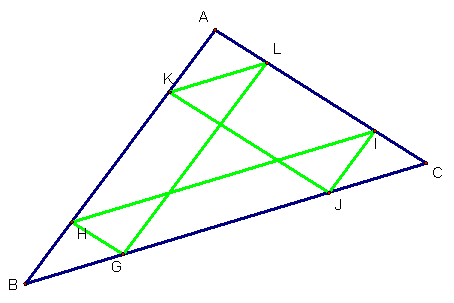
BH +
HK + KA +
And GH + HI + IJ + JK + KL + LG = Barney’s
path
KJ
is parallel to AI and JI is parallel to KA and KAIJ is a quadrilateral. Since the opposite sides are parallel then
KAIJ is parallelogram where opposite sides are also equal.
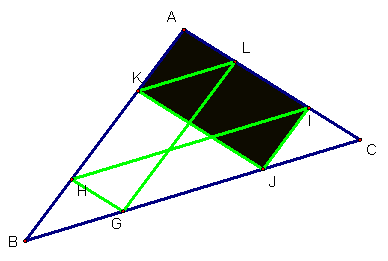
KA=JI and AI= KJ and since AI=AL + LI then
KJ=AL + LI. We can now substitute into
our perimeter equation:
BH +
HK + KA +
BH +
HK + JI + KJ + IC
+ CJ + JG + GB = perimeter of ΔABC
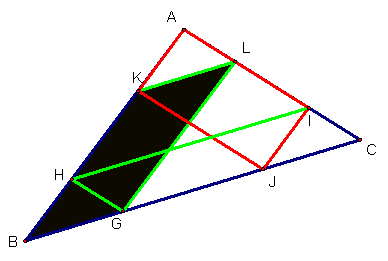
The
same logic follows with quadrilateral BKLG.
Since GL is parallel to BA and KL is parallel to BG then BKLG is a
parallelogram with opposite sides congruent.
BG = KL and BK = GL. Since BK =
BH + HK then GL = BH + HK and the following substitutions can be made:
BH + HK + JI
+ KJ + IC + CJ + JG + GB = perimeter of ΔABC
GL + JI + KJ
+ IC + CJ + JG + KL = perimeter of ΔABC
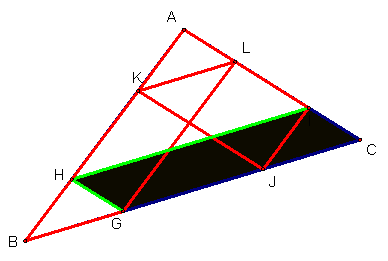
To
complete the substitutions we need to look at quadrilateral GHIC. HI is parallel to GC and GH is parallel to CI
so GHIC is a parallelogram with opposite sides equal. GH = CI and GC = HI and
since GC = GJ + JC then HI = GJ + JC and the following substitutions can be
made:
GL + JI + KJ
+ IC + CJ + JG + KL = perimeter of ΔABC
GL + JI + KJ
+ GH + HI + KL = perimeter of ΔABC
Since
GH + HI + IJ + JK + KL + LG = Barney’s path
then Barney’s path now equals the perimeter of ΔABC which means
that he will always start and end in the same place.