
Summer Tuggle
Assignment
11
Polar Equations
Investigate r= a + b cos(kΘ)
Compare with r= b cos(kΘ) for
various k.
What if cos( ) is
replaced with sin( )?
First let’s
investigate what effect each variable has on the graph. Let’s look at what happens when b and k are 1
and we vary “a”.
On the graph
below we will look at a few cases:
r =
1 + 1 cos(1Θ) r = 2 + 1 cos(1Θ) r = 3 + 1 cos(1Θ)
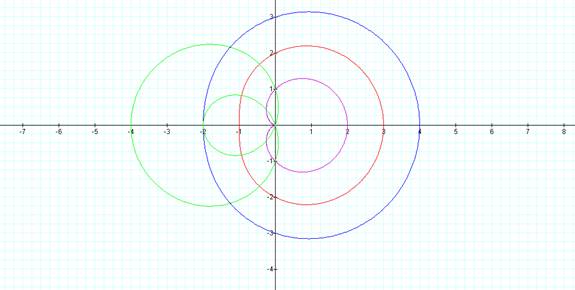
As “a” becomes
bigger, the graph becomes more and more like a circle.
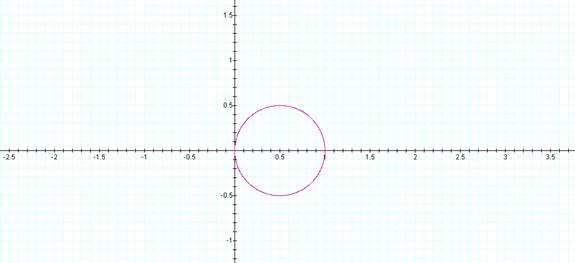
It is interesting
to note that when is “a” is 0 the graphs appears to be a circle with an origin
at (1/2, 0)
If we keep a and
k constant and alter “b” we get another pattern:
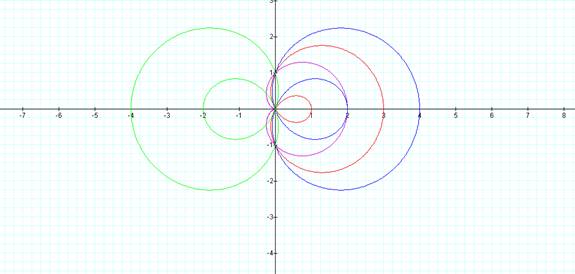
r =
1 + 1 cos(1Θ) r = 1 + 2 cos(1Θ) r = 1 + 3 cos(1Θ)
r = 1
- 3 cos(1Θ)
When a and b are
constant at 1 and k is varied you get the basic n-leaf rose where “k” gives the
number of petals.
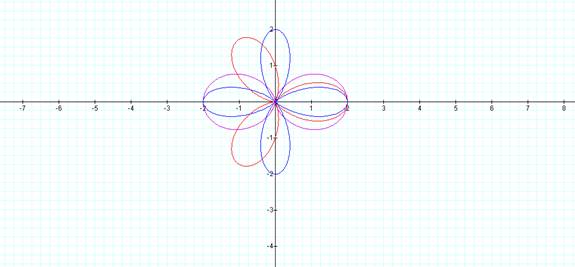
r =
1 + 1 cos(2Θ) r = 1 + 1 cos(3Θ) r = 1 + 1 cos(4Θ)
Changing the size
of a and b but keeping them equal to each other gives you longer petals. 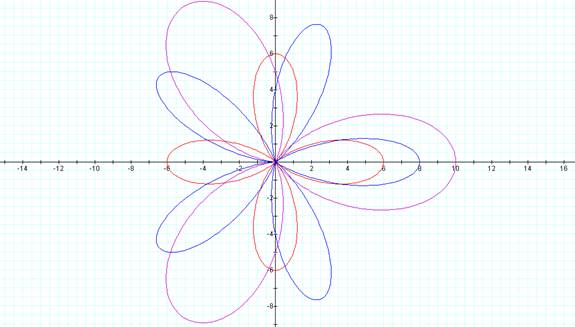
r =
5 + 5 cos(3Θ) r = 3 + 3 cos(4Θ) r = 4 + 4 cos(5Θ)
When a and b are
no longer equal, our rose petals no longer meet at the origin:
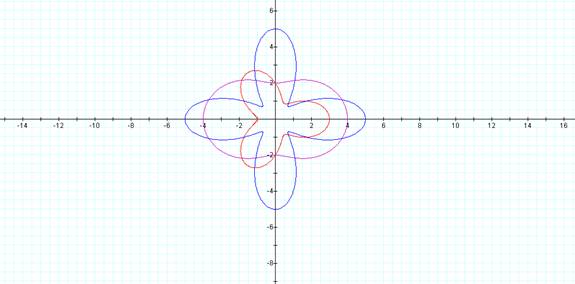
r= 3
+ 1 cos(2Θ) r = 2 + 1 cos(3Θ) r = 3 + 2 cos(4Θ)
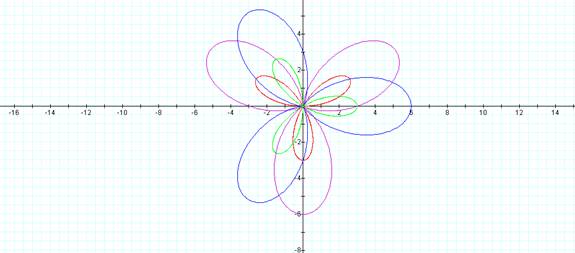
Now let’s compare
r= a + b cos(kΘ) with r= b cos(kΘ)
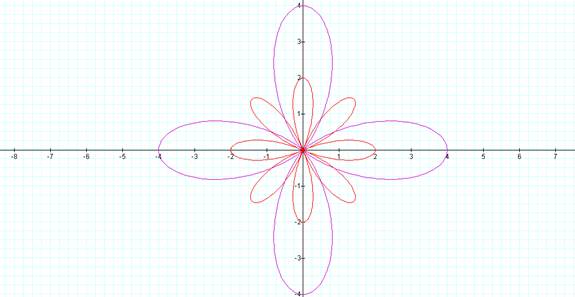
r= 2 + 2 cos(4Θ) r = 2 cos(4Θ)
The purple flower
has 4 stretched out petals as would be expected based on the previous
explorations. The red flower has 8 petals not 4 as would be expected with a k
value of 4. Upon further investigation, I found that in the graph of r= b cos(kΘ) the number of petals follows an interesting pattern. For all even k, the number of petals is
double the k value while for all odd k the number of petals is k.
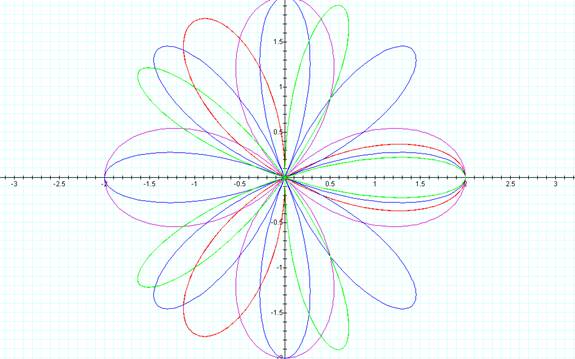
r= 2 cos(2Θ) r= 2 cos(3Θ) r= 2 cos(4Θ) r= 2 cos(5Θ)
When you compare
the graphs of r= a + b cos(kΘ) and r= b cos(kΘ) with r= a + b sin(kΘ) and r= b sin(kΘ) you see that the graph is basically the same except that the
petals have rotated.
r= 3 + 3 sin(3Θ) r= 3 + 3 sin(3Θ)
r= 3 + 3 cos(3Θ) r= 3 cos(3Θ)