
Summer Tuggle
Assignment
6.1
1.
Construct
a triangle and its medians. Construct a second triangle with the three sides
having the lengths of the three medians from your first triangle. Find some
relationship between the two triangles. (E.g., are they congruent? similar?
have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove
whatever you find.
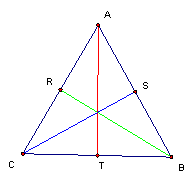
Triangle
ABC is the original triangle. Line
segments RB, SC, and TA are the medians of triangle ABC.
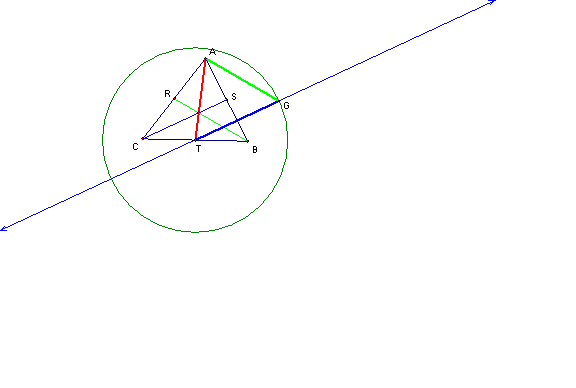
Let
AT act as one side of our new triangle whose side lengths are equal to the
medians of the triangle ABC. From center T create a circle with radius
SC. Then from point T create a line that
is parallel to CS. This radius (TG) will
serve as the second side of our new triangle.
Connect point A and the new point G to get the third side of the
triangle.
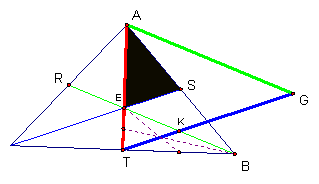
Half
of triangle AGT lies inside the original triangle ABC. Since the medians of a triangle divide the
original triangle into 6 equal parts, the yellow area below is 1/6 of triangle
ABC.

A new triangle, ETB is formed.
The
medians of this triangle can be constructed.
Since TK intersects the other two constructed medians at the centroid, TK is also a median. Therefore, TK bisects EB.
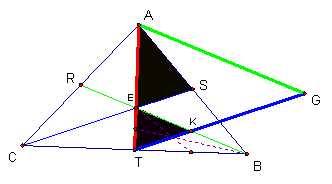
The
purple area, triangle EKT is half of the triangle ETB. Triangle ETB is 1/6 of the original triangle
ABC so triangle EKT is 1/12 of the original triangle ABC.

Point
K and point L are midpoints of their respective sides
thus dividing triangle ESB into a triangle and a trapezoid. The triangle BLK is similar to the original
triangle ESB and scaled by 1/2. This
means that the area of KLB is 1/4 of the triangle ESB and it follows that
trapezoid EKLS is 3/4 of the triangle ESB (which is 1/6 of the triangle ABC). Therefore EKLS is 1/8 of the triangle ABC.
The
sum of the three colored areas (triangle ATL)
(1/6)x + (1/12)x +
(1/8)x is (3/8)x where x is the area of the original triangle ABC. Since

Therefore
the area of triangle ATG is ]2(3/8)x[ which results in
(3/4)x. It can be concluded that the
area of the triangle formed by the medians of another triangle is 3/4 of the
area of the original triangle.
(Dr. Mitch Rothstein
assisted in solving this problem)