Summer Tuggle
Assignment
9
Explore
the pedal triangle that is formed when P is the orthocenter.
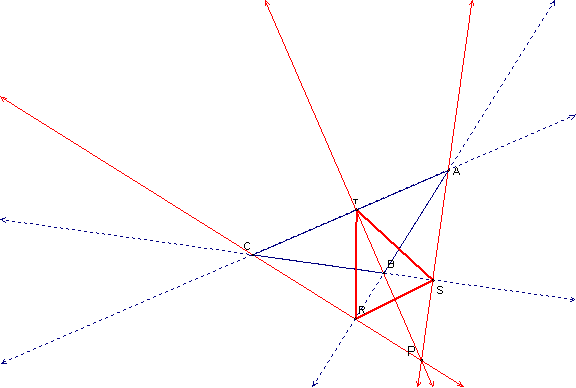
A pedal triangle is formed when you project a point onto
the sides of a triangle. You will drop a perpendicular from point P to each side
of the triangle ABC in order to create points R, S, and T. Connect the new points and triangle RST
becomes the pedal triangle. In this
instance point P is the orthocenter of triangle ABC.
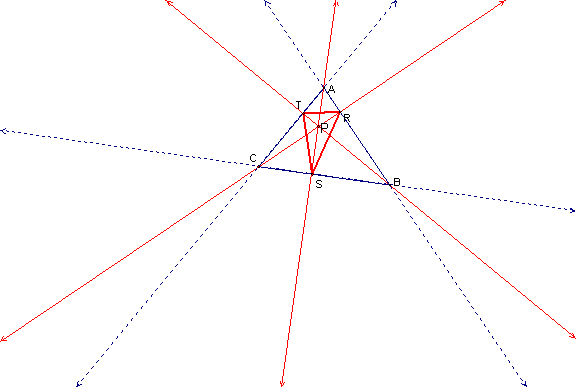
This special case when point P is the orthocenter creates
triangle RST which is the orthic triangle of triangle ABC. A property of orthic triangles is that the
orthocenter of ABC is the incenter of RST.
More specifically, the altitudes of ABC are the angle bisectors of RST.
Since R, S, and T are created from the altitudes of the
original triangle, the pedal triangle collapses when triangle ABC is a right or
obtuse triangle. In the case of right
triangle ABC, the altitudes intersect at a vertex of the original triangle to
form the right triangle.
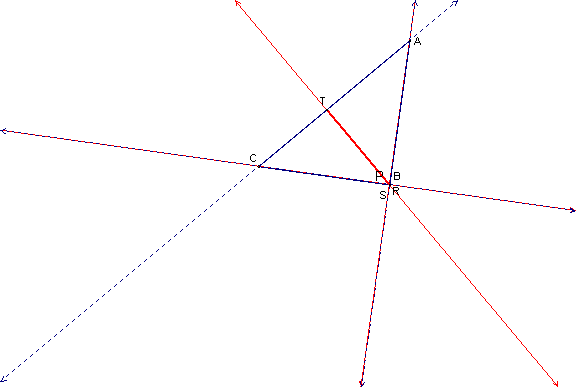
This means that P, B, S, and R are all concurrent. The line connecting the third point of the
pedal triangle (T) to S and R is the angle bisector of the right triangle since
we know that point P (which is also S and R in this case) is the incenter of
triangle RST.
When triangle RST is obtuse two of the vertices of
triangle RST appear on the extension of the respective sides of triangle ABC. Therefore triangle RST is not contained
completely inside of triangle ABC.