

Assignment 11: Polar Equations
by Shawn Broderick
Disclaimer: Some Greek letters don't display with some browers. In that case, p is pi and w is omega.
1. Here we explore polar equations with Graphing Calculator 3.5.
We begin by exploring the given equation:
r = a + b cos (kq), q goes from 0 to 2 pi.
When a, b, k are equal to one, we have...
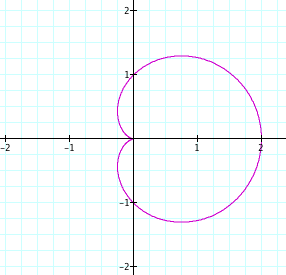
...a cardioid! Or, a 1-leaf n-leaf rose. We next take k = 2:
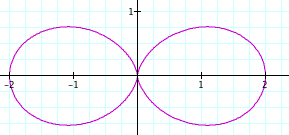
Now we see that there are two leaves. We next take k = 3:
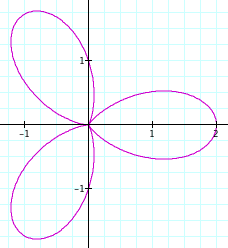
We have the 3-leaf rose. As one may assume, the number of leaves continue to increase as n increases. Here is a fun video illustrating this:
This graph reminded me of graphs that I worked with in abstract algebra. I want to pause for a moment from the problem and talk about a connection to abstract algebra.
This is a key to finding all the solutions to x3 = 1. We know that one is an answer, but because the equation is of degree three, there are two more answers. Here is a graph of the two other answers:
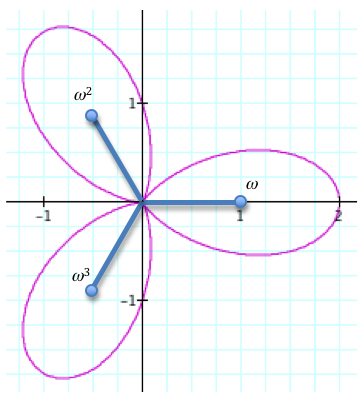
First we look at the graph of 1, which is the answer we know is true. It is labeled as w. If we divide up the polar plane into thirds, as does the 3-leaf rose, we can find the other two answers, thanks to Euler. The next solution is labeled w2. The notation is w2 = e2p i / 3. The length of the segment is one which corresponds to the coefficient of e. The angle around the plane is 2p / 3. To go another third around the plane, we simply add on another 2p / 3 to the angle for w2. We end up with the position for w3. This is equal to e4p i / 3. The amazing thing is, is that when you cube each of these numbers, you get 1. For example, with w2 you can add on another 2p / 3 and then another 2p / 3 and arrive at 1. Same with w3.
Anyway...let's go back to the problem at hand.
We now compare the n-leaf rose with another given equation: r = b cos (kq). Here is a graph of that with b, k = 1.
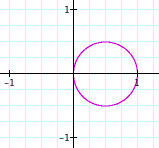
We can see that it is a circle. With higher ks we get (with k = 2, 3):
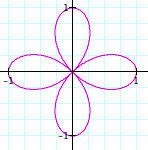
k = 2
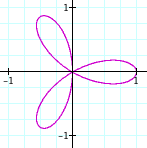
k = 3
Wait...Is is just me or does the k = 2 case look funny? It seems that with this new form of n-leaf roses, the even number is doubled. Let's look at another even and odd case, k = 4, 5:
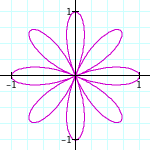
k = 4
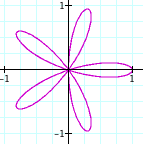
k = 5
Hmm...It looks like the k = 4 case did the same as the k = 2 case. So, we can conclude that it is extremely likely (we say extremely likely because is has not been proven in our argument) that even numbered ks produce double the amount of flower leaves.
The next part of our investigation is to see what happens when cosine is replaced by sine in the equation. For this, we look at:
r = b cos (kq), for b = 1, k = 4, 5 (to compare with the last two examples). Here are the graphs:
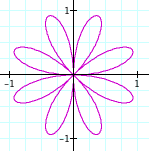
Using sine and k = 4
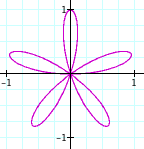
Using sine and k = 5
Well, it looks as if the even double leaf thing happens with sine, too. If we look at the pictures from before and these, we notice that they are the same, except that the leaves are rotated some. They could be rotated a little or a lot, we cannot tell from these pictures.
Just for fun, I looked at replacing cosine with the other trigonometric functions and got some interesting graphs:
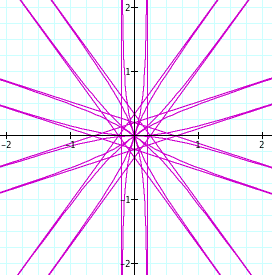
Using tangent and k = 5. (Wow, fun!)
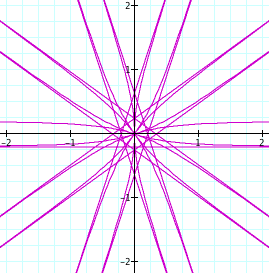
Using cotangent and k = 5. (Notice the slight differences from the tangent example.)
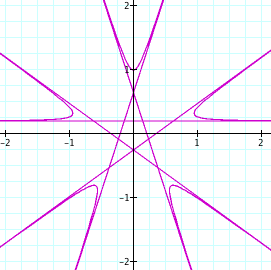
Using cosecant and k = 5. (I really liked this one. Notice the pentagram asymptotes and the hyperbolic-like figures on the outside.)
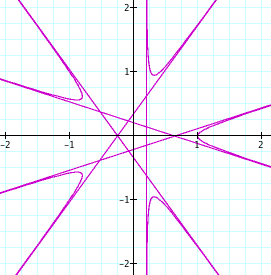
Using secant and k = 5. (Notice that it is just like cosecant, but rotated some.)