Assignment 4: Relationships Among Centers of Triangles

by Shawn Broderick

I have chosen to complete Excercise 5 of Assignment 4. To refresh our memory of the problem, here is the description:

"5. Use GSP to construct G, H, C, and I for the same triangle. What relationships can you find among G, H, C, and I or subsets of them? Explore for many shapes of triangles."

In this assignment, I will investigate the various definitions of the center of a triangle.

1. Centroid (G). The centroid of the triangle is found by connecting the vertices to the midpoint of the opposite side. These lines intersect at a point called the centroid.

2. Orthocenter (H). The orthocenter of the triangle is found by the intersection of lines that are perpendicular to each side and go through the vertices.

3. Circumcenter (C). The curcumcenter of the triangle is found by the center of a circle the circumscribes the vertices of the triange.

4. Incenter (I). The incenter of the triangle is found by locating the center of a circle that inscribes the triangle.

Here is a picture of a scalene triangle with all those centers labeled:

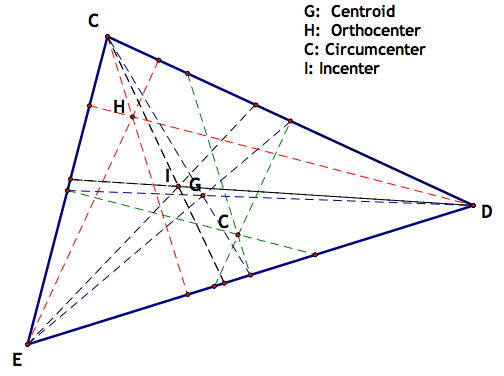
If we show the hidden parts that were required in making this triangle with all the centers, we will come up with something like this:

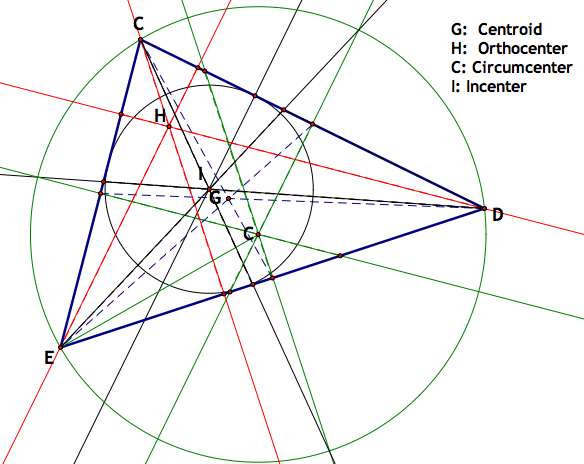
We can identify a few things about the centers based on their constructions. For example, the circumcenter (C) looks low. This is because it is based off of the circle that circumscribes it (green). This is because the longest side is the one that influences the size of the circle, composing a chord near the length of the radius. The incenter (I) and the centroid (G) are close to the center, but (H) is also high. It looks like that depends on the angle side CE and side CD make with each other. One other curious item we can see from showing all the work involved in constructing these centers, is that the angle bisectors of all the angles in the triangle intersect the vertices and the circumscribed circle.

We are required to explore the centers of many different triangles. The next type of triangle is an iscoceles triangle:

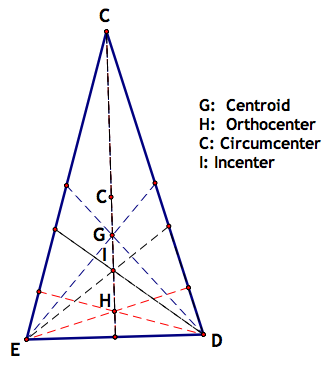
I found it interesting to see how these centers lined up. From lowest to highest, the centers go H, I, G, and C. Why is that? It looks to go in reverse order from the triangle above. Well, let's take a look at the hidden things again:

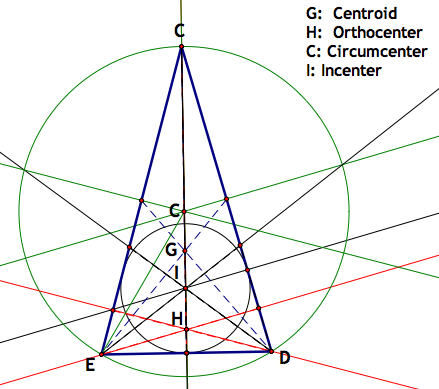
I can see that the center C is positioned higher on an iscoceles triangle because the longer sides move the circumscribed circle upward, thus moving the center upward. The center H is low, but not sure why. Notice again that the angle bisectors intersect the circumscribed circle at the same point the perpendicular lines to the midponts of the sides do.

Let's look at another type of triangle, the equilateral triangle. Any guesses as to where the centers are? Let's see:

All the centers are locted in the same location when the triangle is equilateral. It looks like the center of the triangle depends on the angle measures of the angles and the length of the sides. If all are equal, then this is the result. Here is this case with all work shown:

Notice that all of the lines that determine the centers of the triangle are together, right on top of each other. It shows to me that they are all viable ways to find the center of a triangle.

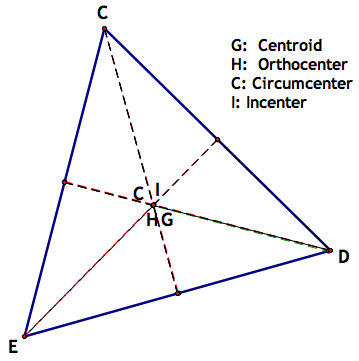
Our next triangle is a long, skinny one:

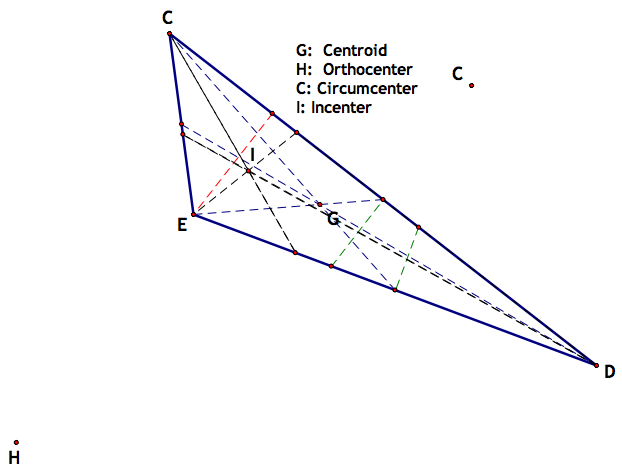
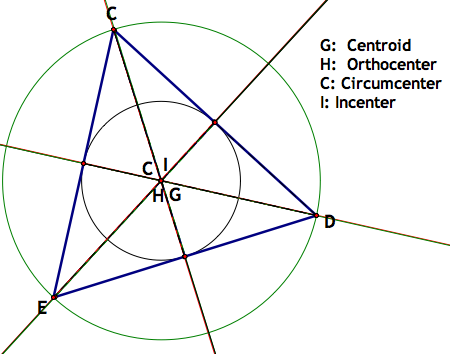
The first thing that one notices is that the center H and the center C fall apart, meaning that the aren't in the triangle at all. Center I and Center G, still hold fairly well. Let's see all work and look at why this may be:

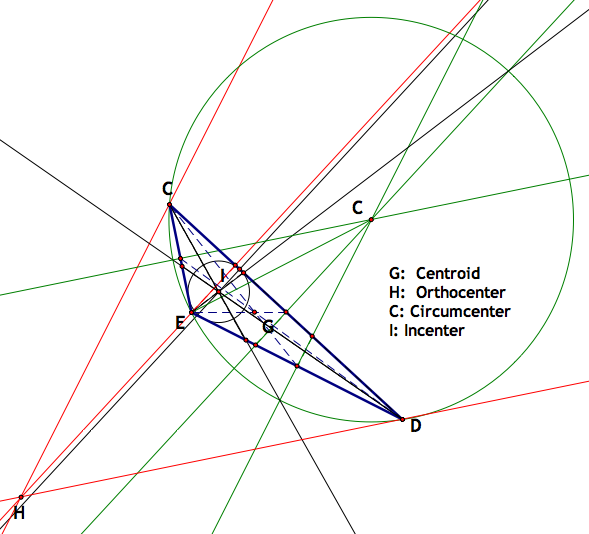
The orthocenter has only one side that maintains its perpendicularity with the opposide side. By moving the angle E around in GSP, we can see that center H breaks down when E goes above 90 degrees. The same story applies to center C, because it is also based off of perpendicular lines.

This leads us to our final triangle, a right triangle (based on angle E being 90 degrees):

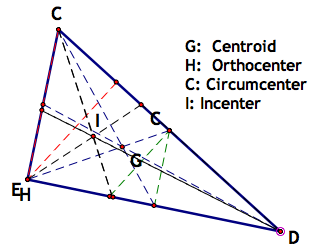
Notice that center H and center C now lie directly on the triangle. Center H on vertex E and center C on side CD. Let's look at the work:

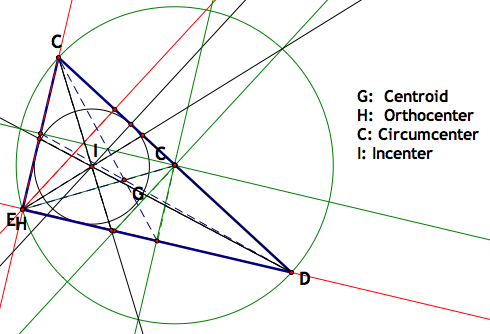
Again, because center H and center C deal with perpendicular lines, they are kind of opposites here. They make a rectangle:

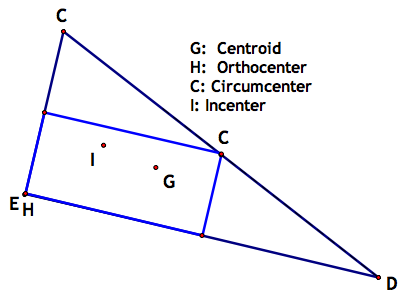
There are probably a million more things one can discover about these centers, but this has been my investigation.