Assignment 9: Pedal Triangle and Triangle Centers

by Shawn Broderick

Pedal Triangle Problem refresher:

Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.

Example, when Pedal Point is outside the triangle:

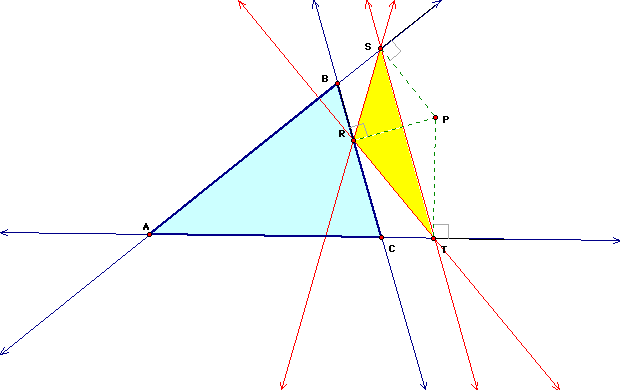
Example when Pedal Point is inside the triangle:

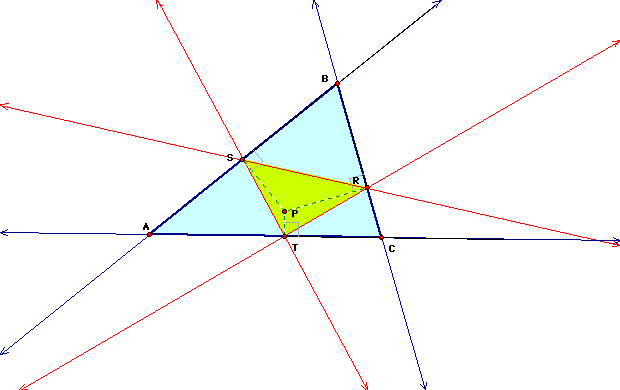
I have chosen to investigate a few applications of the Pedal Triangle when it is in line with various centers of triangles.

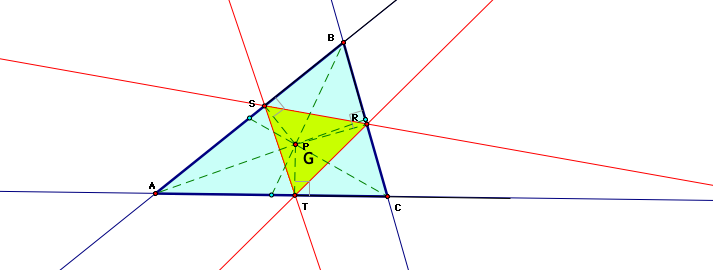
2. What if pedal point P is the centroid of triangle ABC?

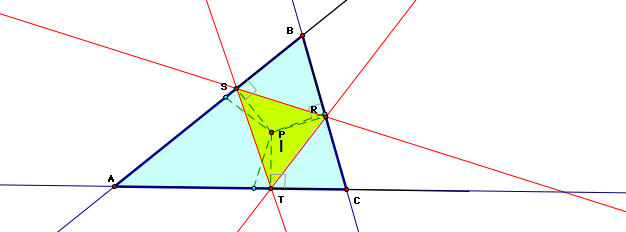
3. What if . . . P is the incenter . . . ?

4. What if . . . P is the Orthocenter . . . ?

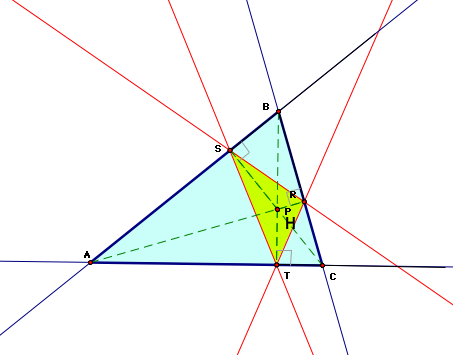
Even if outside ABC?

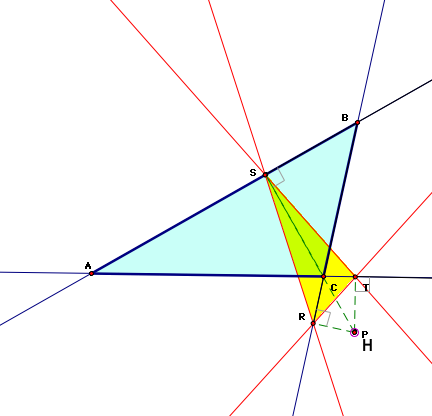
5. What if . . . P is the Circumcenter . . . ?

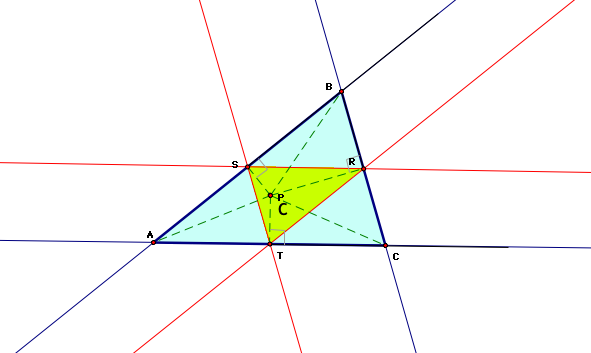
In the picture above, I saw some interesting things. I first noticed that the extended lines of the pedal triangle seemed parallel to the extended lines of the original triangle when the pedal point is on top of the circumcenter. I say seemed because I haven't proved it yet. This occurs even when both triangles are modified so that the circumcenter and the pedal point are outside of the original triangle as shown below.

If they are indeed parallel, we can prove that the area of the pedal triangle is 1/4 of the total area of the bigger triangle. We could also prove that triangle BSR is congruent to triangle SAT, RTC, and SRT. This would be true for the pedal triangle below, too.

Here is the GSP file that shows that the areas of all the triangles are the same: pedalptcircumctr_invest.gsp

Even if outside ABC?

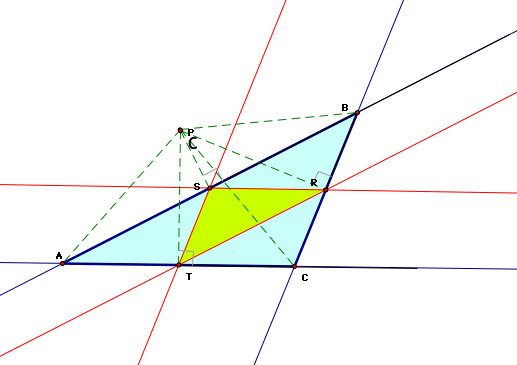
6. What if . . . P is the Center of the nine point circle for triangle ABC?

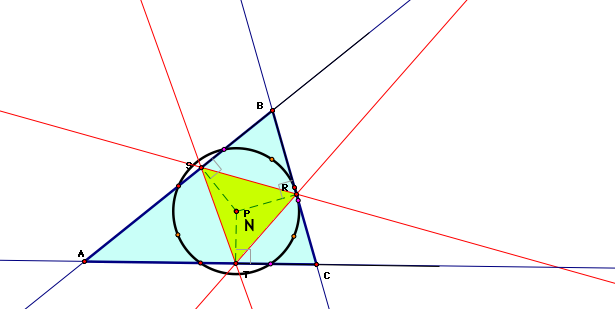
This pedal triangle also has interesting properties. It looks as if triangle BSR is congruent to triangle RTC. There must also be a relationship between those two triangles and triangle SAT. Perhaps the two smaller triangles hav the same area as triangle SAT. However, an investigation in GSP yielded no such relationships. See pedalpt9ptcirc_investigation.gsp