
Essay 1: Model of the Solar System
Question: Using the Geometer's Sketchpad (GSP), can we build a model of the solar system? What mathematics do we need to know?
Where do we start? Well, the Internet is a good source of information, and we need all the statistics that we can have about the planets. Using a search engine, I found the this site of Solar System Data.
We are in search of key statistics that will allow us to plot the orbital path the planets take around the sun. As we peruse the tables of the planetary data, we can see that the key statistics for our needs lie in the maximum and minimum distances to the sun (i.e., the aphelion and perihelion, respectively). This means that the paths of the planets around the sun (i.e., their orbits) are not perfect circles. They can be considered as ellipses where the sun is one of the foci.
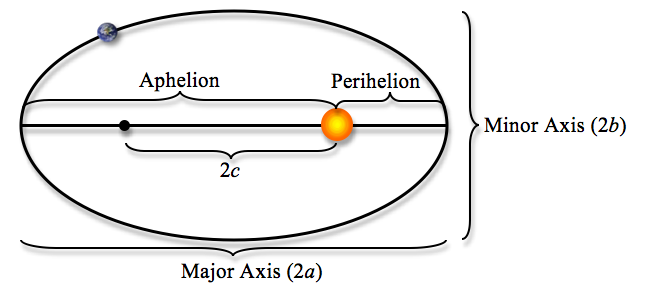
Therefore, the first point of mathematics we must call up is our knowledge of ellipses. The general formula for an ellipse is:
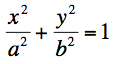
where a is the length from the center to the edge of the ellipse along the major axis (i.e., the longer axis) and b is the distance from the center to the edge of the minor axis. Therefore, if we add the maximum and minimum distances from the sun, we will find the length of the major axis, 2a. Then we divide that number by two and square it to get a2. Finding b is the harder part, but there is a formula for that as well. It comes from the helpful relationship of c2 = a2 – b2. The variable c is the distance from the center of the ellipse to the foci.
In GSP, we can only graph with formulas in the form of y = ... So the next mathematical idea we need to use is algebra in order to solve for y. Here is a way to do this:
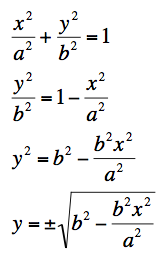
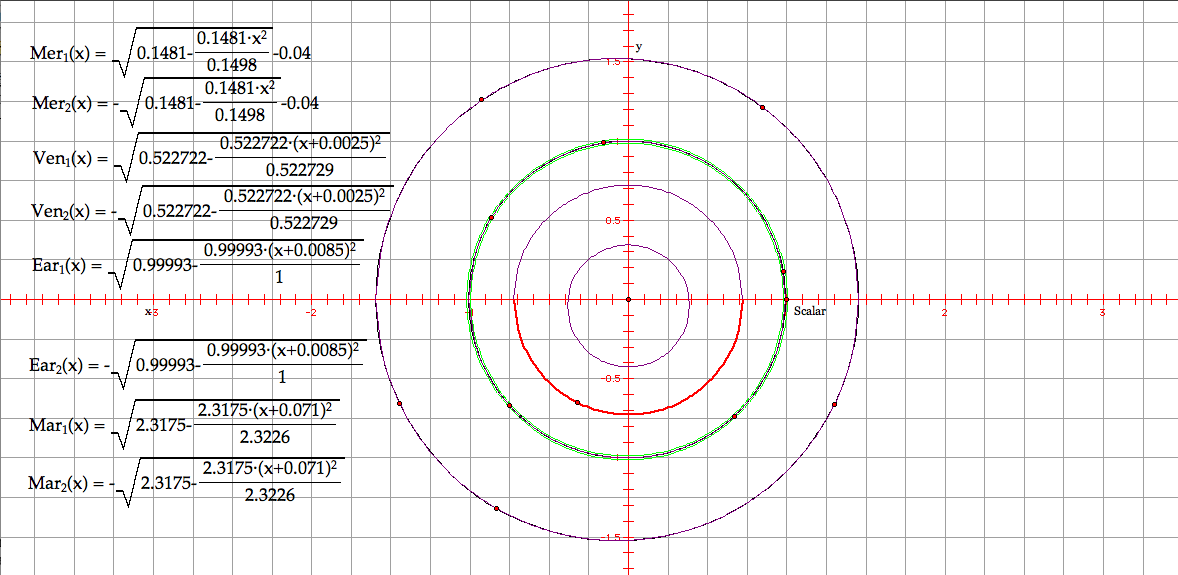
Because GSP does not know how to handle the plus or minus symbol we must enter the equation as two separate ones, one positive (with no sign) and one negative and graph each separately.
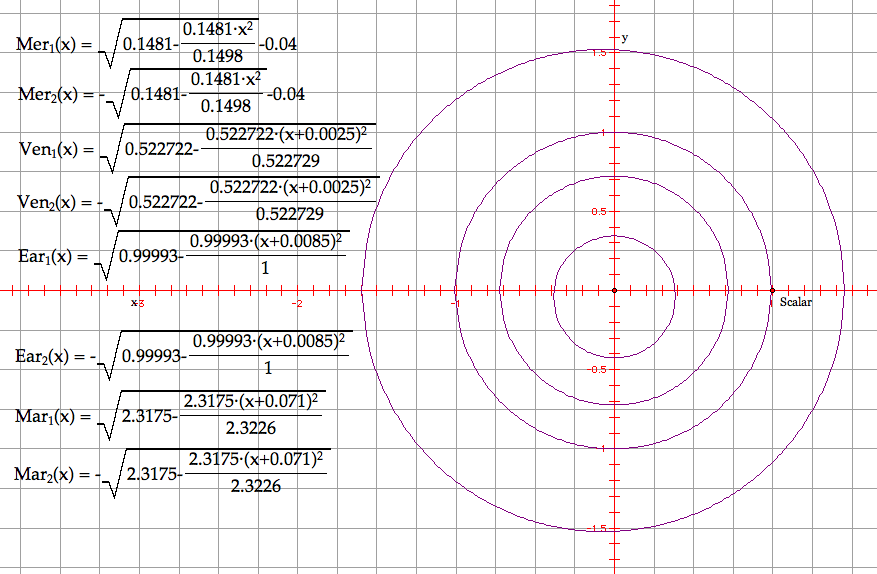
We can now begin by finding the exact formula for the orbital path of Mercury. Mercury has an aphelion of 0.467 AU and a perihelion of 0.307 AU. The mean (a) would be 0.387 AU. Now, by subtracting the perihelion distance from the mean, we will find the length 2c. Therefore, 0.387 – 0.307 = 0.08, and then c would be half of that, which is 0.04. We can find b by using our formula of the relationship of a, b, and c. Therefore, we have (0.04)2 = (0.387)2 – b2, and b = .385. We also need to make the center of our graph the position of the Sun. So, the entire ellipse needs to be shifted a length of c, or in this case 0.08. For Mercury, we will shift it down 0.08 AU and thus put "- 0.04" at the end of our equation since it will be a vertical shift down. (We will see why this is later on.)
Therefore, the equation that we will use for the ellipse that represents Mercury's orbit is:
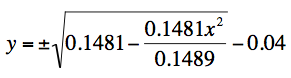
Our next planet is Venus. Venus has an aphelion of 0.728 AU and a perihelion of 0.718 AU. The a would be 0.723 AU. Then 2c would be 0.723 – 0.718 = 0.005. Half that is 0.0025. The corresponding b is 0.722996 because the c is so small. Because a and b are so close, then the orbit of Venus is very nearly a circle. We will go ahead and shift the ellipse to the left 0.005 AU even though it will probably not be perceptible. We do this by adding 0.005 on to the x inside the parentheses. The formula for the orbit will be:
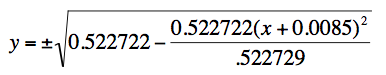
For Earth, we have an aphelion of 1.017 AU and a perihelion of 0.983 AU. The a would be 1 AU. The 2c would be 0.017, thus c is 0.0085. The corresponding b is 0.99993. Again the orbit is nearly a circle and again we will shift the ellipse to the left by 0.0085 AU. The formula for the orbit will be:
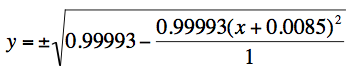
For Mars, we have an aphelion of 1.666 AU and a perihelion of 1.382 AU. The a would be 1.524 AU. Our 2c would be 0.142, and c is 0.071. The b is 1.522. We will shift the ellipse to the left by 0.071. The formula is:
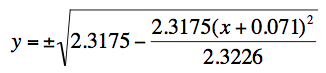
Once we have graphed these equations, we will have a GSP file somewhat like this:
We now must create circles that will represent the planets moving along their orbits. However, the planet circles will probably not be able to make complete revolutions along two separate equations. Therefore, we must take these half-circles and make them continuous circles. The tool of "Conic Through Five Points" will be perfect for this. Use it on all the orbits. Here is an intermediary picture:
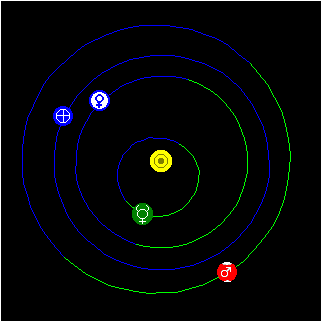
Once all the complete ellipses are made, we now hide the five points and examine this picture from Solar System Live website that shows the relative positions of the inner planets as of 2/23/09 (This is why we subtracted from Mercury's orbit ellipse on the outside and added to everyone else's, so it would look somewhat like the real thing.):
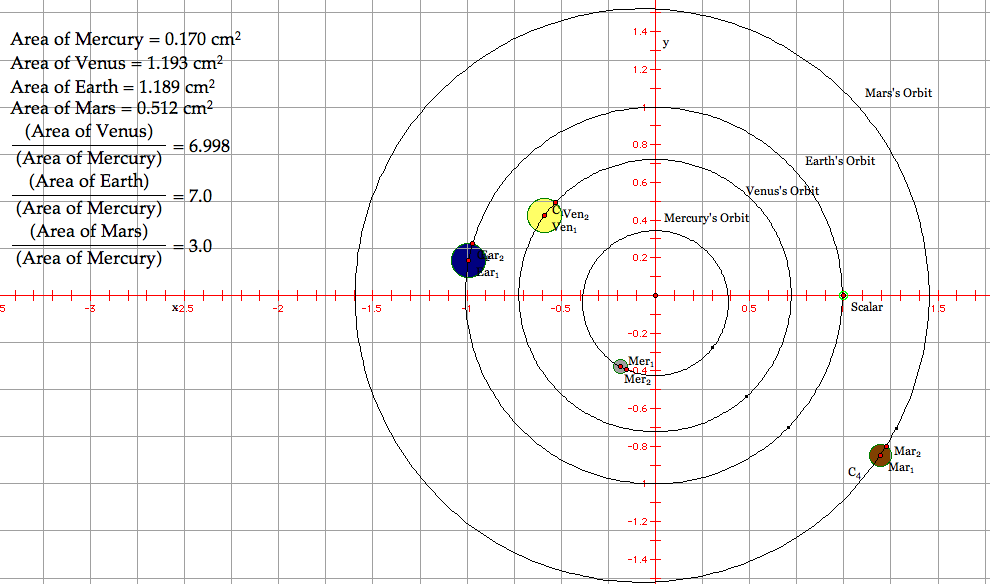
We also must consider, as much as we can, the relative size of the planets. On GSP, we need to have a small circle represent Mercury (2440 km radius) and larger ones for Mars (3390 km), Venus (6052 km), and Earth (6371 km). If we calculate the area of a circle that represents Mercury, using the given radius, and we take this as the unit 1, we can find the areas of the circles that represent the other planets and find corresponding ratios. We see that the ratio of Mercury to Venus and Earth is 1:7. The ratio of Mercury to Mars 1:3. Construct the interior for all planets (circles). Mercury's color should be gray, because it is cratered and has no atmosphere. Venus should be colored "Banana" from the "Other" category, becuase it's clouds are that color. Earth should be dark blue, and Mars should be about "Mocha." Here is a sample GSP sketch of our project so far:
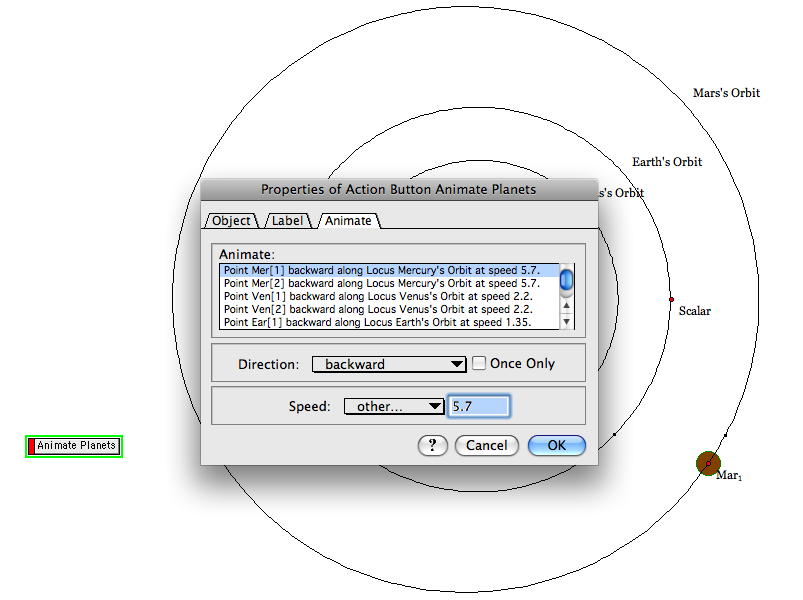
We now need to use an action animation button to revolve the planets around at relative speeds. We now find the relative speeds by using the siderial period (i.e., each planet's "year" in Earth days). From our solar system data website we find that Mercury's year is about 88 days, Venus's 225, Earth's 365, and Mars's 687. To find relative speeds, I used the reciprocal of each number of days and multiplied that by 500. So, the speed of Mercury is 5.7, Venus 2.2, Earth, 1.35, and Mars, 0.75. So, we select all the points that determine the circles and then add the animation button. Here is a picture of what we can do:
We now have our solar system!

Here is the gsp file: essay1.gsp