Centers of triangles
by
Hyeshin Choi
1. Centroid
The centroid of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. So I first took midpoints of each side, then constructed segment from opposite vertex.The geometric centroid (center of mass) of the polygon vertices of a triangle is the point which is also the intersection of the triangle's three triangle medians. The point is therefore sometimes called the median point. The centroid is always in the interior of the triangle.

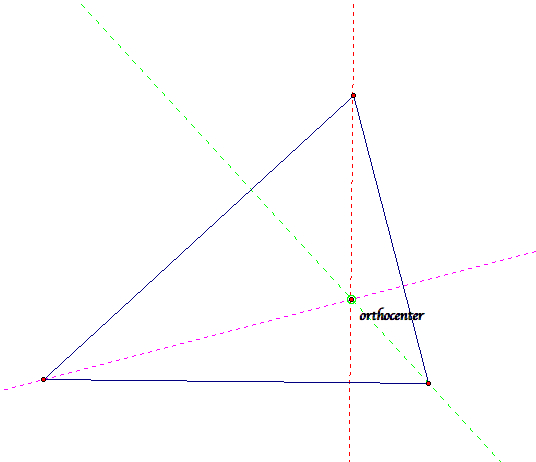
2. Orthocenter
The altitude of a triangle is a line which passes through a vertex of the triangle and is perpendicular to the opposite side. There are therefore three altitudes possible, one from each vertex. It turns out that all three altitudes always intersect at the same point - the so-called orthocenter of the triangle. The orthocenter is not always inside the triangle. If the triangle is obtuse, it will be outside. To make this happen the altitude lines have to be extended so they cross. Adjust the figure above and create a triangle where the orthocenter is outside the triangle. Follow each line and convince yourself that the three altitudes, when extended the right way, do in fact intersect at the orthocenter.
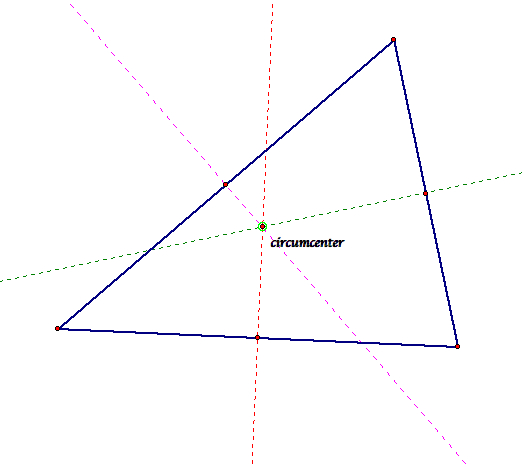
3. Circumcenter
The three perpendicular bisectors all come together in one point, called the circumcenter of triangle ABC. The circumcenter is equidistant from the three vertices, and so the common distance is the radius of a circle that passes through the vertices. It is called the circumcircle.