For Assignment 12 we will explore the Fibonacca Sequence!

We will use f(n) = f(n-1) + f(n-2) and we are asked to construct the ratio of each pair of adjacent terms in the Fibonnaci sequence. What do you think happens as our value of n increases?

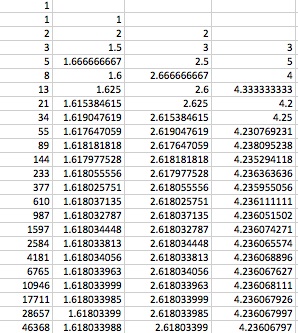
Here in our chart we can see the outcomes of our operations! In the second column I divided b2/b1 and we can see that they are converging to 1.61803399.And what isthat number...Why it is the Golden Ratio!

Then for the third column I once again divided and got the same outcome! Except this time that are converging to 2.61803399...which is the golden ratio squared!

And what do you think happened for the third column? The same thing and the number converged to 4.23606798 which is the golden ratio cubed!

What do you think happens when we change our numbers? Instead of f(0)=1 and f(1)=1 I used f(0)=2 and f(1)=4. Here is what the outcome was...

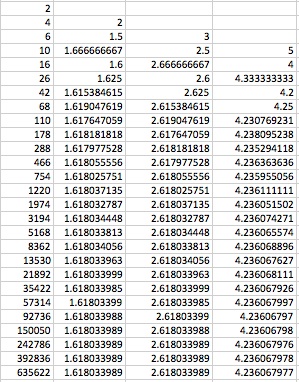
If you closely look at it you see that they still converge to the same thing. Cell two goes to the golden ration...cell three goes to the golden ratio squared and cell four to the golden ration cubed! Why is this so?

RETURN