ASSIGNMENT 3

QUADRATIC AND CUBIC EQUATIONS

BY:

DEBORAH ECKSTEIN

For Assignment 3 I have chosen to look at the equation y = ax^2 + bx + c.

First let's change our values of a ,keeping our b and c at 1, and see what happens to our graph. Here we let a=-3,a=-2,a=-1,a=0,a=1,a=2,a=3.

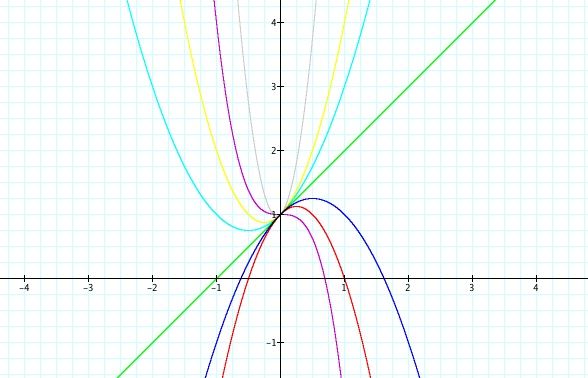
In our graph there are many conclusions that we can draw:

1.) When our value of a is negative our parabola open down and when a is positive the parabola always opens up.

2.) When we have a = 0 we no longer get a parabola but we get a line. Why do you think this is?

Now let's change our c value, keeping a and b constant, and see what happen to our graph. Let c=-3,c=-2,c=-1,c=0,c=1,c=2,c=3.

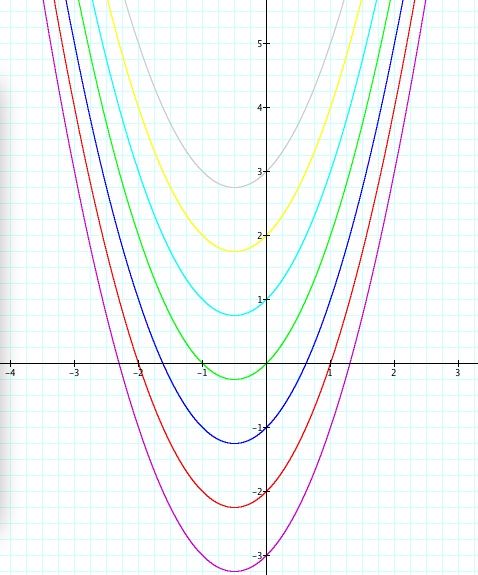
Here we can see that the value of c changes, all of our parabola do not go through the point (0,1) anymore. Why is this so?

Now let's keep a and c constant at 1 and have different values of b. Here is a graph with the set values of b=-3,b=-2,b=-1,b=0,b=1,b=2,b=3.

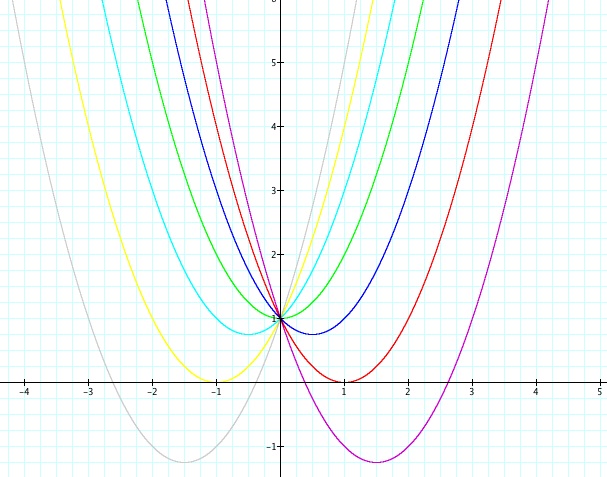
Looking at the graph we can see that all of the parabolas, no matter what our b value, goes through the point (0,1). Here are some other facts that we can gather:

1.) For b < -2 the parabola will intersect the x-axis in two points with positive x values(look at our purple line to see this)

2.) For b = -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root at the point of tangency.

3.) For -2 < b < 2, the parabola does not intersect the x-axis -- the original equation has no real roots.

4.) For b = 2 the parabola is tangent to the x-axis

5.) For b > 2, the parabola intersects the x-axis twice to show two negative real roots for each b.

Now let's find the locus of our equation and see what we will get. In order to find the locus of our equation we have to complete the square!

With our locus equation we can assume that it will be opening downward because of the negative out front. Let's graph our locus on the same graph as our changing b graph.

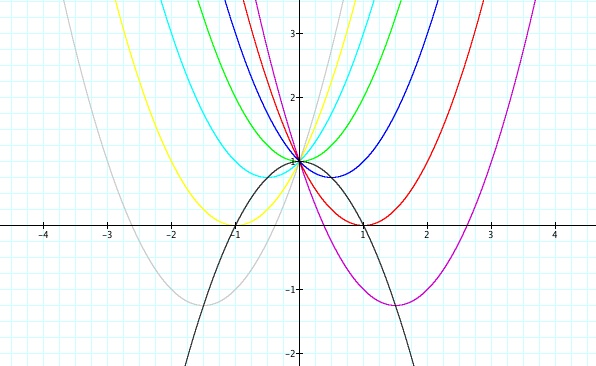
Here we can see our locus is in fact a parabola that opens downward!

RETURN