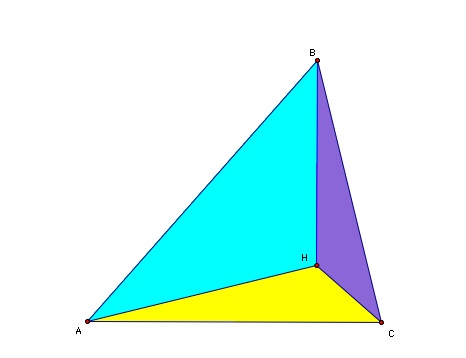
For assignment 8 we start out with any triangle ABC and then construct the orthocenter and label it H.

By constructing the orthocenter of triangle ABC we have formed three new triangle: HBC, HAB, HAC. We will now construct the orthocenters of each of these three triangles.

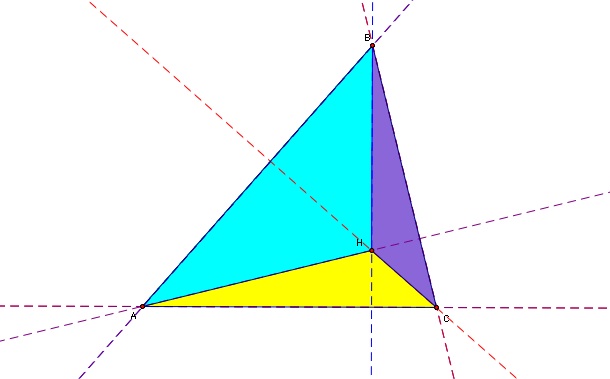
Now we will construct the circumcirlces of triangles ABC, HBC, HAB, and HAC.

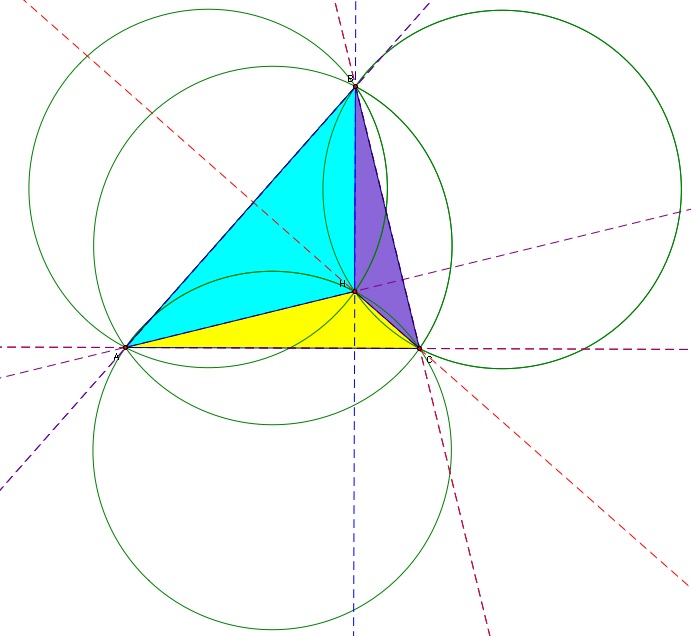
What do we notice from the constructions that we have made so far? For starters we can see that our circumcircles around the three triangles, HBC, HAB and HAC all intersect at point H (our orhocenter of triangle ABC).

What do you think would happen if we were to take any vertex on our triangle ABC and moved it to where the orthocenter H is located? Let's move our vertex and check it out. For this I choose to move our vertex B.

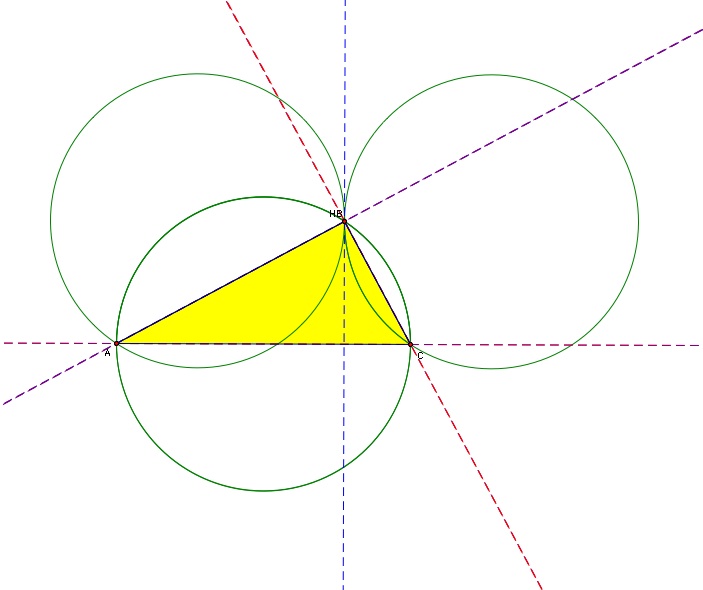
It forms the triangle AHC, making our original orthocenter H one of the vertices. If we look we can see that it produces the same circumcircles. Here is a GSP file for our original triangle. You can move each vertex and notice that you will get the same result but for a different triangle. CLICK HERE

_______________________________________________________________________________________________________________________________________________________________

For Assignment 8 I have also chosen to investigate problem 12.

It states that given any triangle ABC construct the orthocenter H. Then let points D, E, and F be the feet of the perpendiculars from A, B, C. Prove the following:

1. (HD/AD) + (HE/BE) + (HF/CF) = 1

2. (AH/AD) + (BH/BE) + (CH/CF) = 2

Here is our image created in GSP.

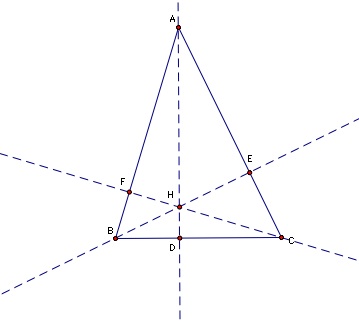
I. PROVE: (HD/AD) + (HE/BE) + (HF/CF) = 1

For proof 1 we will use the areas of the three triangles (BHA, BHC, CHA) that we created by constructing the orthocenter H.

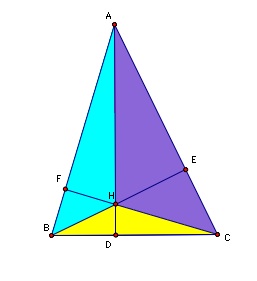
Notice that we can find the area of our triangle ABC in three different ways:

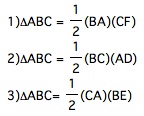
And we know that the area of the whole triangle ABC can be found by adding the area of the smaller triangles together. Therefore we can write the equation:

To see a calculation proof in gsp click here! What do you notice happens when you make the triangle obtuse?

II. PROVE: (AH/AD) + (BH/BE) + (CH/CF) = 2

We now by segment addition that we can say

AH = AD - HD

BH = BE - HE

CH = CF - HF

We can now substitute that into our equation (AH/AD) + (BH/BE) + (CH/CF) = 2

To see a calculation proof in gsp click here! And look once again at what happens when you make the triangle obtuse!

RETURN