

ASSIGNMENT 9
PEDAL TRIANGLES
BY:
DEBORAH ECKSTEIN
Assignment 9 asks us to explore pedal triangles. To do this we will let triangle ABC be any triangle. Then if P is any point in the plane, the triangle formed by constructing the perpendicular to the sides of ABC locate the three points R, S and T that are the intersections of the perpendicular lines to the (sometimes extended) lines that form the triangle. Therefore, the triangle RST is the Pedal Triangle for Pedal Point P. Let's look at a picture of a pedal triangle!
Here is an image for a pedal point that is outside of our triangle.
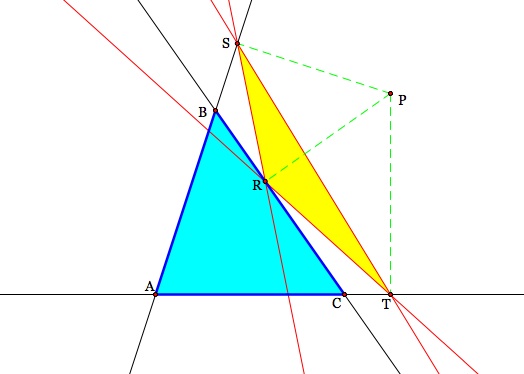
Here is an image for a pedal point that is inside of our triangle.
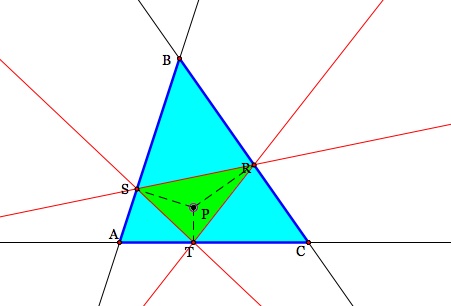
HERE is a GSP file that has a script tool for the creation of pedal triangles. This way you can move the pedal points around to different locations.
Let us look at what may happen if our pedal point is the centroid, incenter, orthocenter, or one of the vertices of the triangle ABC.
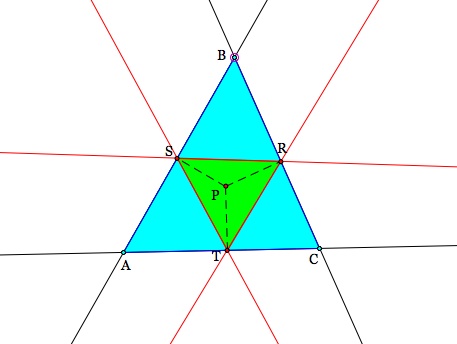
1) Let the pedal point be the CENTROID of the triangle. Remember that the centroid of a triangle stays inside of the triangle whether the triangle is obtuse or acute. So what do you think will happen with our pedal triangle? The same thing perhaps?
Here is the pedal point as a centroid in an acute triangle:
Here is the pedal point as a centroid in an obtuse triangle:
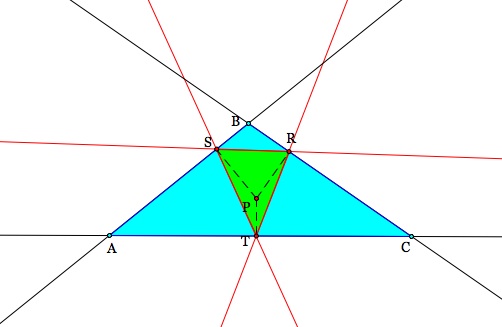
Notice that what we predicted was right. Despite whether the triangle is obtuse or acute, when the centriod is the pedal point our pedal triangle stays inside of our triangle.
HERE is a gsp file for you to explore some more triangle shapes with our pedal point being a centroid!
2) Let the pedal point be the INCENTER of the triangle. Remember that the incenter of a triangle is the point in the triangles interior that is equidistant from all three sides of the triangle.
Here is the pedal point as the incenter a triangle:
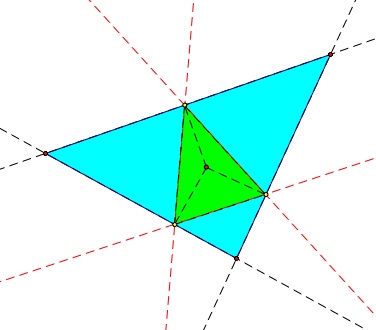
Notice that it almost seems like the pedal point would also create the circumcenter of the triangle! Let's take a look...
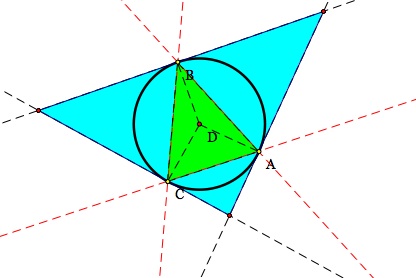
We are right! Here is a gsp file so that you can move the triangle around and see if you make any more discoveries!
3) Let the pedal point be the ORTHOCENTER of our triangle. Remember that an orthocenter can be inside or outside of our triangle depending on whether or not you have an acute or obtuse triangle. Will this affect where our pedal triangle is? Also what kind of triangle do you think this pedal triangle will create?
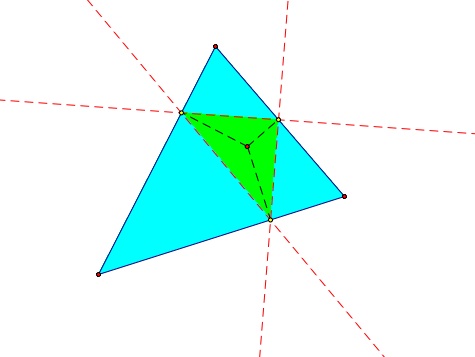
Here is our acute triangle (notice that our pedal triangle stays inside of our triangle):
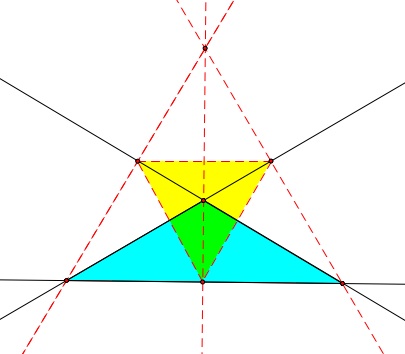
Here is our obtuse triangle (notice that our pedal triangle comes out of our original triangle):
Here is a gsp file so that you can move the triangle around and possibly find more cool observations!
4) Now let's explore what may happen when our pedal point one of the vertices of our triangle:
We end up without a triangle. Why do you think this is?
Here is a gsp file for this case!
There are many more cases that you can explore with the pedal triangle. What do you think would happen if the pedal point was the circumcenter, or possibly the center of a nine point circle.