Lesson 1 Objectives:
1. Understanding the undefined terms: point, line, plane.
2. Understanding the defined terms: collinear, coplanar, and intersection.
2. Drawing representations of points, lines and planes.
************************************************************************************************************************************************************
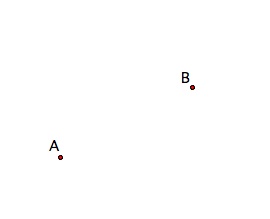
The simplest figure in geometry is referred to as a point. It does not have a certain size and is often represent with a dot and labeled using capitol letters. Points are in all geometric figures and we define space to be the set of all points. Below are the points A and B.
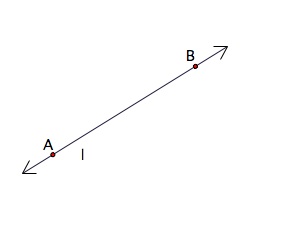
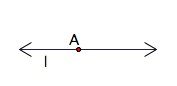
Another familiar geometric figure is a line. A line extends in two different directions with no end. A line itself does not have any thickness and is labeled using a lower case letter. If you know that two points are on the line you can also define it using those two points. Below is line l or ![]() .
.
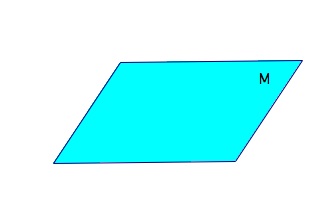
A geometric plane is suggested by a floor or wall. It extends with no end or edges and has no thickness, but when we draw a plane we normally draw it as a four-sided figure. Normally planes are labeled with capitol letters, just like points. Below is plane M:
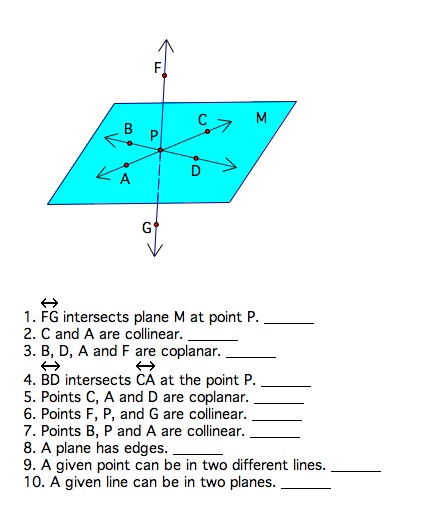
Collinear points are points all in one line and non collinear points are points that are not on one line. Below points A, F and B are collinear and points G and H are non collinear.

Coplanar points are points all in one plane and non coplanar points are points that are not in the same plane. Below points B, C and E are coplanar, points D and A are coplanar but points E and D would not be coplanar.
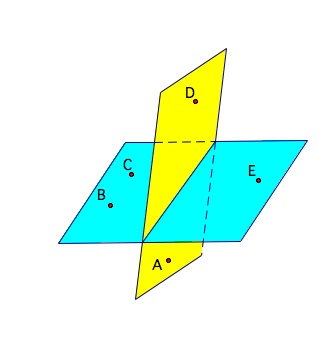
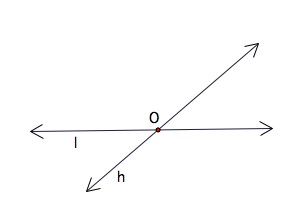
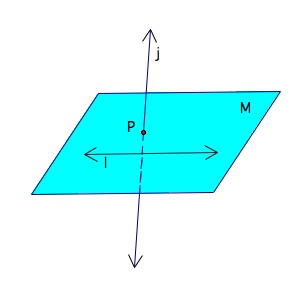
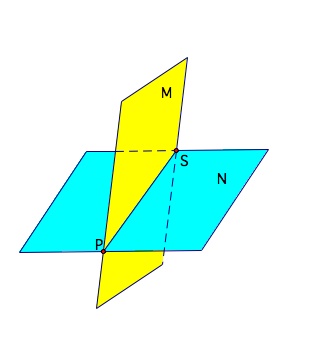
The intersection of two figures is the set of all points that are in both figures. (The dashes in the diagrams indicate parts hidden from view in figures in space). Below are a few examples of intersections.




***********************************************************************************************************************************************************
Student Exercises:
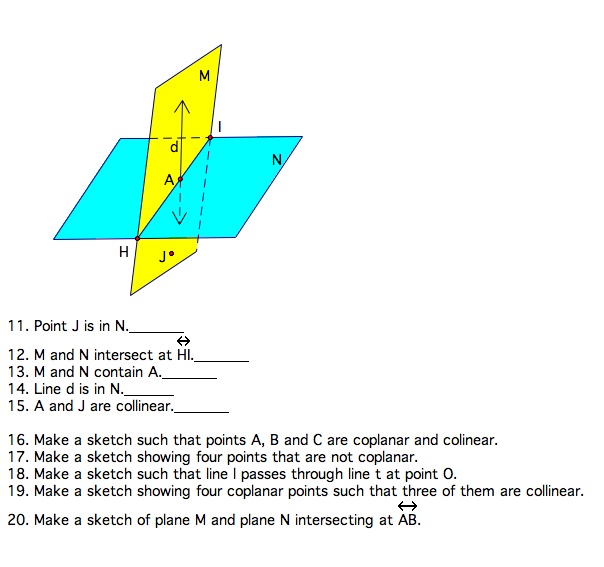
Given the following figures classify each statement as true or false.