Lesson 2 Objectives:
1. Learn how to use symbols for lines, segments, rays, and distances.
2. Finding distances.
3. Segment Addition Postulate
**************************************************************************************************************************************************************
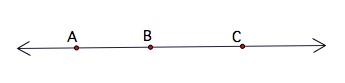
Points can lie between each other on a line. In the following diagram point B is between point A and point C. Also, point B in on line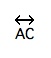 
.
A segment is a line that has two endpoints and contains all the points between the two endpoints. From the above diagram,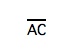 
is a segment that has endpoints A and C.
A ray is a line that has one endpoint.
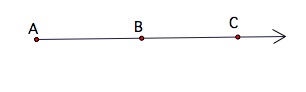
Ray AC is denoted by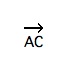 
and consists of segment 
and all other points, such as B. The endpoint of is A which is the point named first.
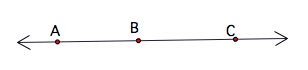
Opposite rays are rays that go off in opposite directions. In the following diagram, 
and 
are opposite rays.
Ruler Postulate:
1.The points on a line can be paired with the real numbers in such a way that any two points can have coordinates 0 and 1.
2. Once a coordinate system has been chosen in this way, the distance between any two points equals the absolute value of the difference of their coordinates.
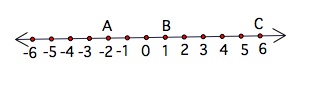
From the above diagram point A is paired with -2, point B is paired with 1. To find the distance between two points, or the length of that segment, take the absolute value of their coordinates. Notice distance can not be negative and that is why absolute value is used.
To find the length of the segment take the absolute difference of the coordinates of point A and point C.
Segment Addition Postulate:
If B is between A and C, then AB + BC = AC.
In geometry two objects that have the same size and shape are called congruent.
Congruent segments are segment that have equal lengths. If we wanted to show that segment and 
were congruent we would denote it,
.
The midpoint of a segment is the point that divides the segment into two congruent segments. In the diagram below B would be the midpoint and 
.
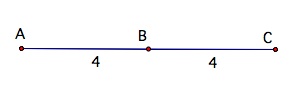
A bisector of a segment is a line, segment, ray, or plane that intersects the segment at its midpoint.
***********************************************************************************************************************************************************
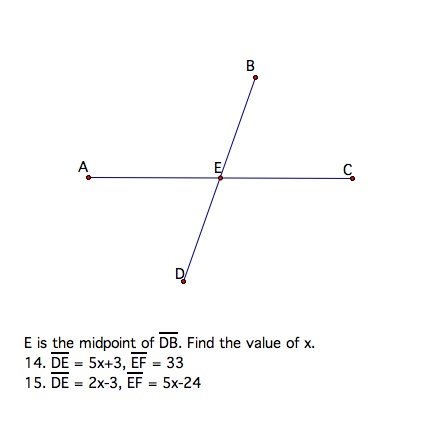
Student Exercises:
