Lesson 4 Objectives:
1. Postulates and Theorems
************************************************************************************************************************************************************
For this lesson we are going to go over the remaining theorems from the chapter and put all of the key ideas together.
Postulate 1:
A line containing at least two points; a plane contains at least three points not all in one line; space contains at least four points not all in the one plane.
Postulate 2:
Through any two points there is exactly one line.
Postulate 3:
Through any three points there is at least one plane, and through any three non collinear points there is exactly one plane.
Postulate 4:
If two points are in a plane, then the line that contains the points is in that plane.
Theorem 1:
If two lines intersect, then they intersect in exactly one point.
Theorem 2:
Through a line and a point not in the line there is exactly one plane.
Theorem 3:
If two lines intersect, then exactly one plane contains the lines.
Remember that a postulate is a statement that we accept without proof and a theorem is a statement that has been proved.
***********************************************************************************************************************************************************
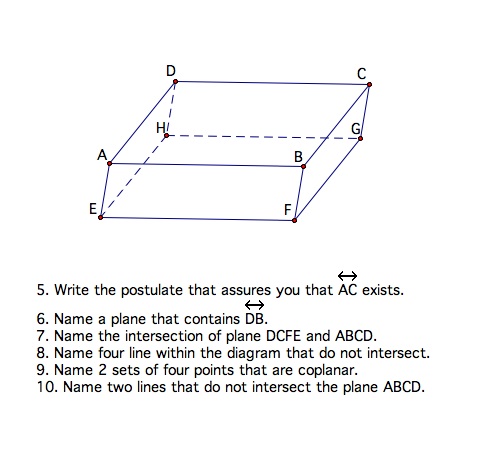
Student Exercises:
State whether it is possible for the figure described to exist.
1. Two points both lie in each of two lines.
2. Three points all lie in each of two planes.
3. Three non collinear points all lie in each of two planes.
4. Points A and B lie in a plane.
a. What can you say about the line AB?
b. State the postulate that supports your answer to part (a).