MATH 7210 FINAL

Deborah Eckstein

For the final project I have decided to break down some of the material in chapter 5.1 on reflections and translations into material that high school geometry students could use.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Reflection

A reflection in line m maps every point P to a point P' such that:

1. If P is not on the line m, then m is the perpendicular bisector of PP'.

2. If P is on line m, then P'=P.

Now let's look at a visual of a reflection:

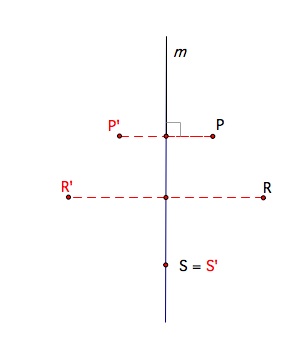
A reflection in a line is an isometry. To remind yourself , an isometry is a transformation that preserves distance. Let's take some time to prove this!

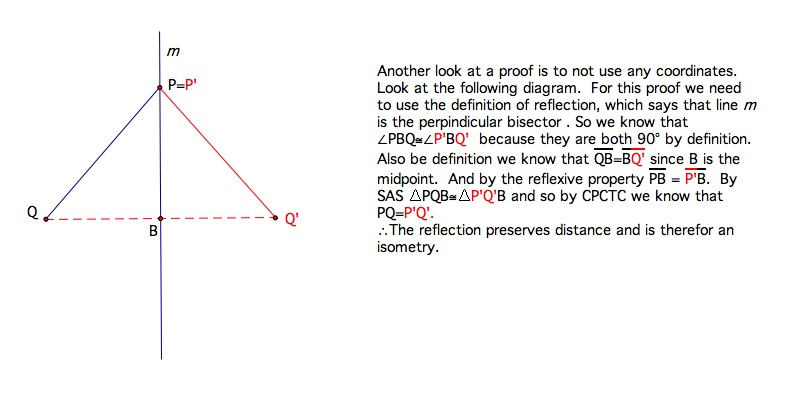
Now that we have proved that a reflection is an isometry we can say that a reflection

1. Preserves distance

2.Preserves angle measures

3. Preserves area of a polygon

In other words under a reflection distance, angle measurements and area are invariant.

What about orientation? Let's take a look at what happens with orientation when we have a reflection.

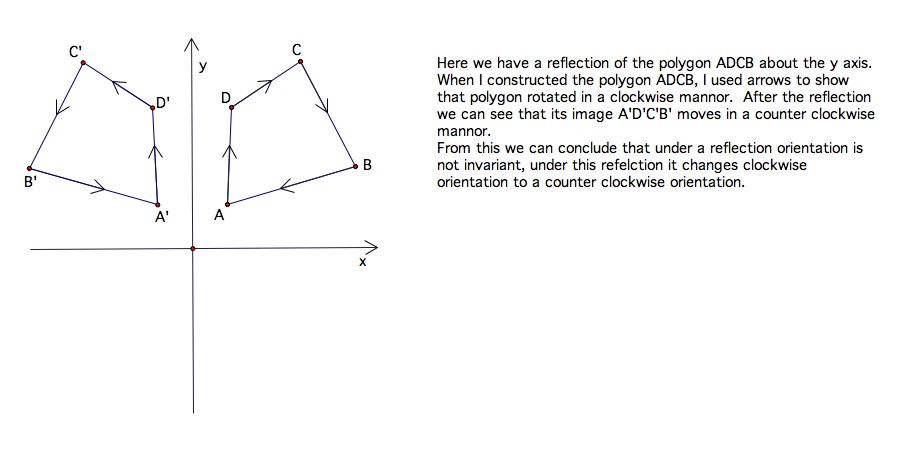
Here is an example that let's try to work through:

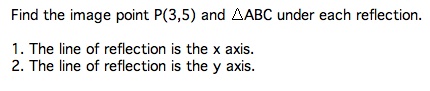
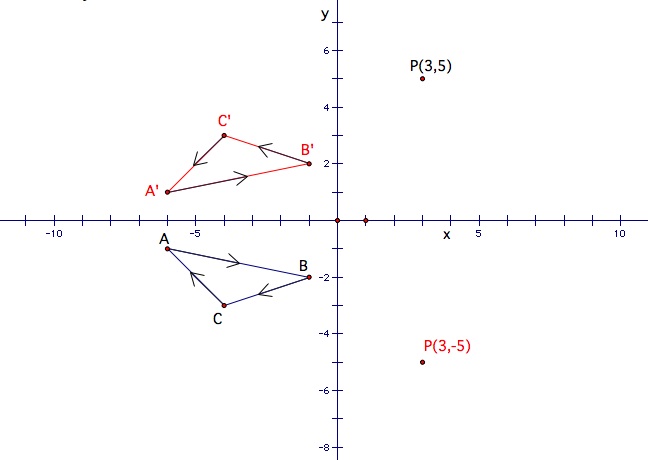
Now try number 2 on your own!

Here is some homework that you can try on your own!

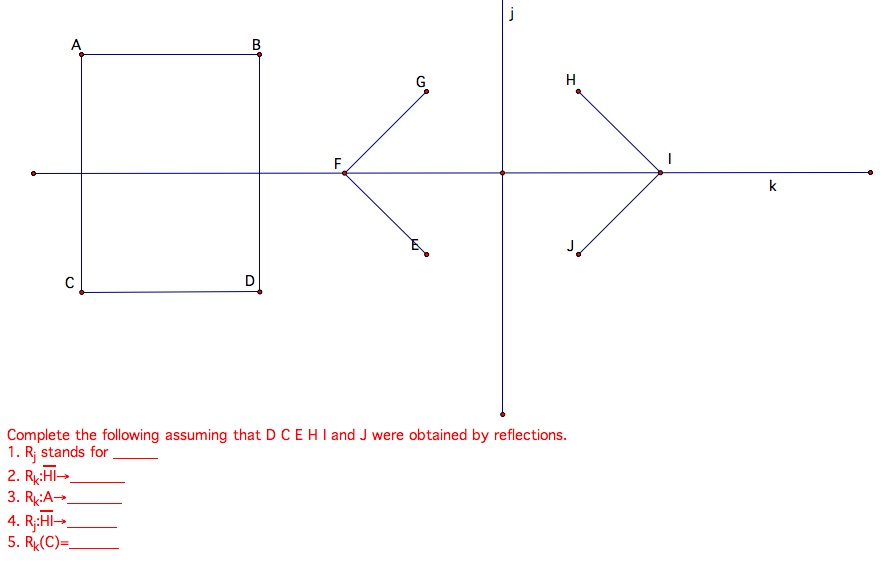
Copy down the following figures and draw the image by reflection in line k.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

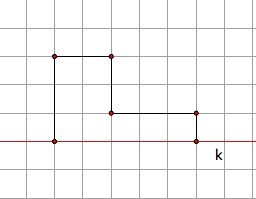
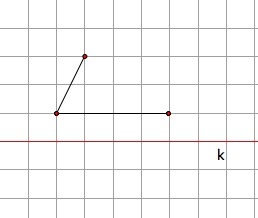
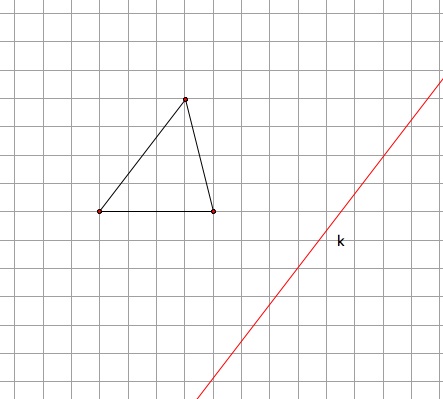
Translations

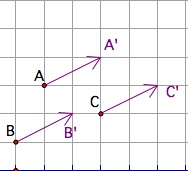
A translation is a transformation that glides all points of the plane the same distance in the same direction.

Therefore if a transformation maps A to A', B to B' and C to C', points A B and C glide along parallel segments, and AA'=BB'=CC'. Let's take a look at a picture to see what exactly is going on.

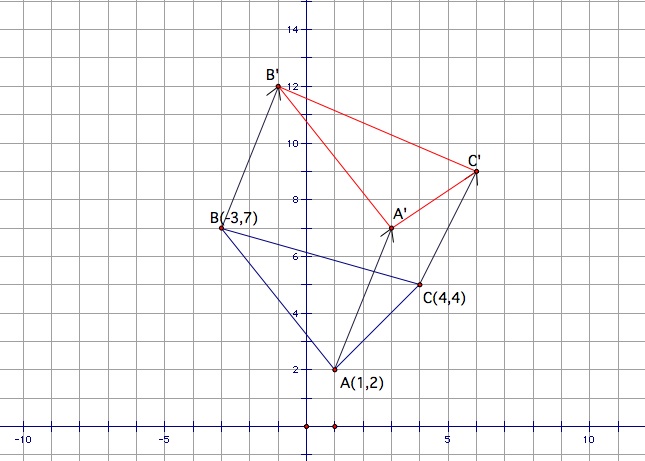
Let's try an example to see what a translation looks like. Let's start out with a triangle with coordinates A(1,2), B(-3,7) and C(4,5). Given these points consider a translation where every point glides 5 units up and and 2 units to the right. To find out where the points move we could think of it in two ways. First we could use the vector (2,5) to indicate the translation. Or we could think of it as a coordinate expression:

Using this coordinate expression we could find the three points that A B and C move to.

From this we can set up a basis for all translations. Given a point (x,y) and and vector (a,b) we can describe the translation using the following coordinate expression:

T:(x,y)-(x+a,y+b).

Just like a reflection is an isometry and translation also is!

let's look at the general case to proof that a translation is also an isometry.