ASSIGNMENT 4

LINEAR FUNCTIONS

BY:

DEBORAH ECKSTEIN

For assignment one I decided to work problem #2. This problem asks us to make up two functions, f(x) and g(x), and to then explore the graphs of:

i) h(x) = f(x) + g(x)

ii) h(x) = f(x) [ g(x)]

iii) h(x) = f(x)/g(x)

iv) h(x) = f(g(x))

I will initially make f(x) = 3x + 2 and g(x) = x + 1

Here are the two functions graphed. ( note that the pink is our f(x) and the red is our g(x))

Now let us explore i - iv and the calculations they require.

i) h(x) =f(x) + g(x) = 4x + 3.

ii) h(x) = f(x)[g(x)] = (3x + 2)(x +1) = 3x^2 + 5x + 2

iii) h(x) = f(x)/ g(x) = 3x + 2 / x + 1

iv) h(x) = f(g(x)) = 3x + 5

NOW LET'S GRAPH THESE FUNCTIONS AND THE OPERATIONS WE PUT ON THEM:

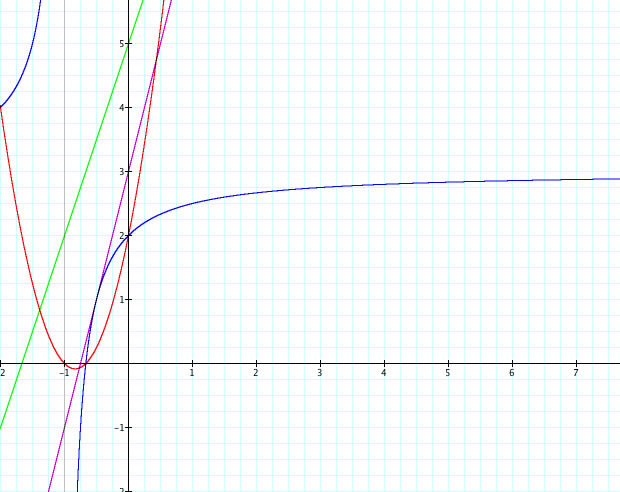
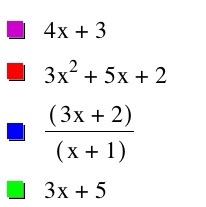
Here we can see the graphs of the four new functions we have created using the operations. With the f(x) + g(x) we get a line with positive slope, with f(g)(g(x)) we get a parabola that opens up, with f(x)/g(x) we get a hyperbola, and with f(g(x)) we get another line with positive slope! NOTICE that our original functions both had positive slopes and so our two lines ended up having positive slopes as well. This is because when adding, multiplying or dividing by two positive numbers your results will always be a positive number. So it is safe to say that if we start with two positive sloped functions and incorporate the given operations on them, we will always get a positive slope.

Now let us look at two functions that both have negative slopes. Let f(x) = -2x - 1 and g(x) = -3x - 4

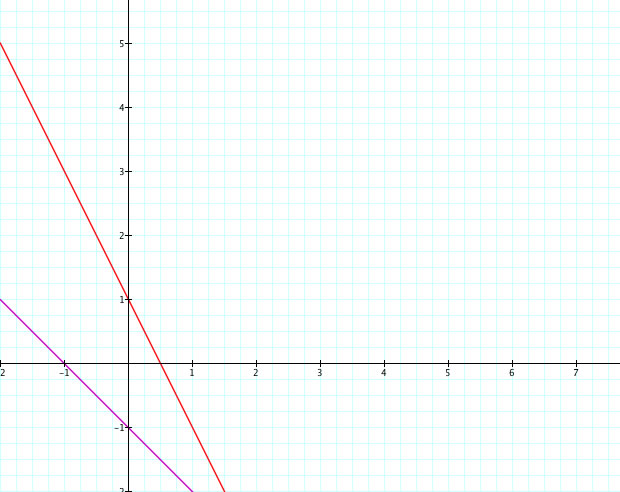
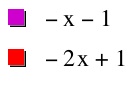
so we can see when we apply the calculations i - iv we get:

i) h(x) = f(x) + g(x) = -3x

ii) h(x) = f(x)(g(x)) = 2x^2 + x - 1

iii) h(x) = f(x) / g(x) = (-x-1) / (-2x+1)

iv) h(x) = f(g(x)) = 2x - 2

NOW LET'S GRAPH OUR NEW FUNCTIONS:

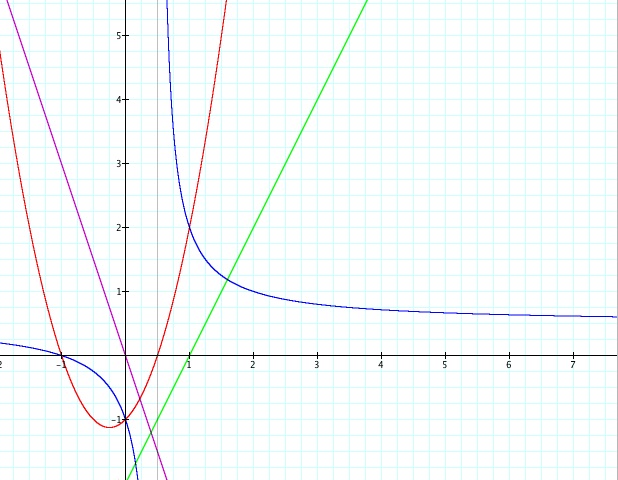
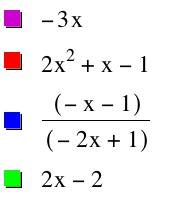
Here we can see the graphs of our four functions that we created. Look at how when we add the two functions together we still have a negative slope because adding two negatives, you still get a negative. But let's look at what happened when we multiplied the two functions together. Since we multiplied two negative numbers together we got a positive number in front of our x^2 and hence we got another parabola that opens upward just like our two (positive) previous functions. Also, when we took the composite we multiplied two negative numbers together and so we got a line with a positive slope.

So now let's alternate and use a function with positive slope and one with a negative slope. Let f(x) = 2x + 3 and g(x) = -3x + 1

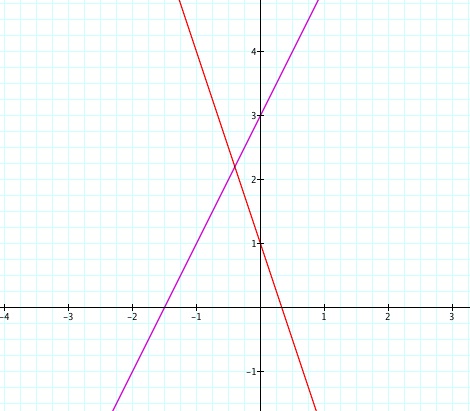
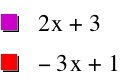
so we can see when we apply the calculations i - iv we get:

i) h(x) = f(x) + g(x) = -x + 4

ii) h(x) = f(x)(g(x)) = -6x^2 - 7x + 3

iii) h(x) = f(x) / g(x) = (2x +3) / (-3x + 1)

iv) h(x) = f(g(x)) = -6x + 5

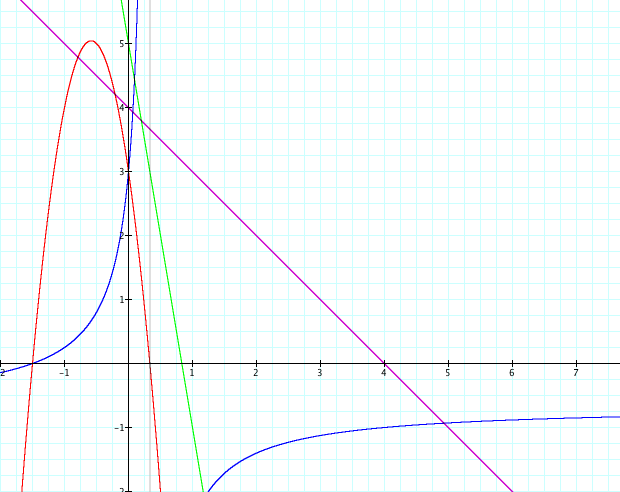
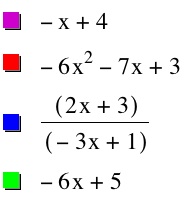
Looking at our graph now having alternate slopes we see that when we added the two functions together we came out with negative slope. This however can not always be true and for this particular problem it just so happens to be negative. Say we had a negative slope of 1 for our first function and a positive slope of 3 for our second function. What would happen then? Our slope would be positive. So for adding of two alternate slope functions you can not always be sure of what the slope of the resulting line will be. It depends on the coefficients! When we multiplied our functions we got a parabola opening downward. This will always be our case because by multiplying a positive and a negative you will always get a negative. And for our f(x)/g(x) we still got a hyperbola and for f(g(x)) we get a line with a negative slope. This will always happen because when we take the composite we will multiply a positive number by a negative number and that always gives us a negative number!

RETURN