For Assignment 4 we are asked to look at some basic triangle geometry. So first let's draw a triangle that will become our basic triangle for all of my explorations in this assignment:

I first choose to look at the centroid of a triangle. A centroid of a triangle is the intersection of the triangles three medians ( a median being the line segment from a vertex of one angle of the triangle to the midpoint of the opposite side).

Now let's draw in the medians and label the point where the intersect!

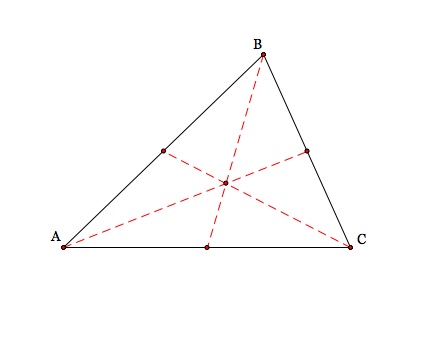
We now have a centroid for our triangle ABC. Let's look at what may happen to the centroid if we change our triangle around!

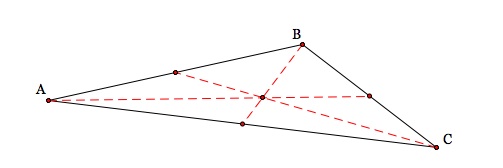
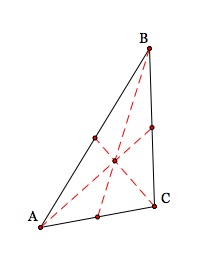
Notice that for our obtuse and acute triangles the centroid is always inside the circle!

Click HERE to open a gsp file so that you can move the vertex around yourself and see that the centroid never leaves the inside of a triangle!

Do you think that also holds for the orthocenter of a triangle. Let's see...

The orthocenter of a triangle is the point of intersection of the altitudes. So we will start with our original triangle and construct the altitudes and label the intersection.

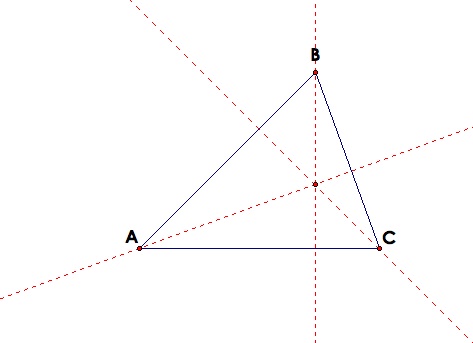
Now we have our orthocenter so let's see what happen when we move our triangle around.

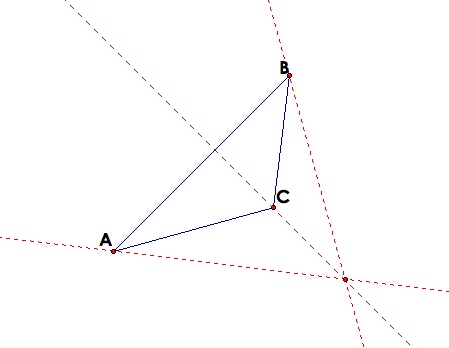
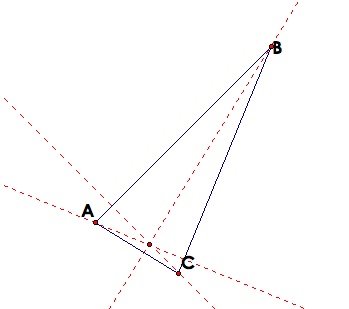
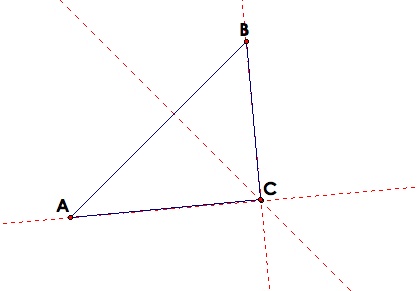
Now we can see that the orthocenter of a triangle can be anywhere. It can be inside the triangle, outside the triangle(for obtuse triangles) and it can lay on the triangle!

Click HERE to open a GSP file so that you can explore further and see that the orthocenter can be anywhere!

RETURN