

Given a triangle ABC, find the point D such that line segments AD, BD, and CD trisect the area of the triangle into three regions with equal areas.
We know that the centroid of a triangle is that point which is the intersection of the triangles three medians. So I am going to assume that point D will be the centroid of the triangle. Let's construct a triangle and its centroid and see if I am in fact right.
To construct the centroid of a triangle:
1. Construct any triangle and label it ABC.
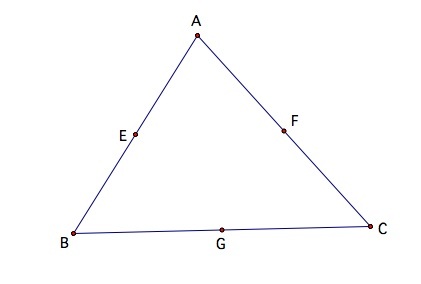
2.Then construct the midpoint of BA and label the midpoint E, then construct the midpoint of AC and label it F and construct the midpoint of CB and label it G.
3. Finally, connect each midpoint to the opposite angle. For example, construct a line segment from angle A to point G. Label the point of intersect D.
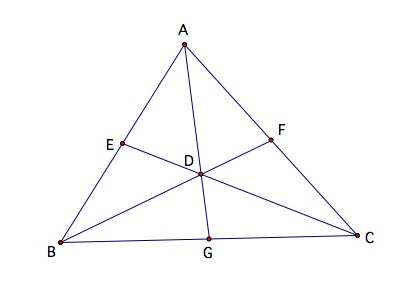
The original problem is to find point D such that AD, CD, and BD trisect the area of the triangle. So let's explore some in GSP and see if we are in fact right that point D must be the centroid. First I am going to look at the areas of the six triangles that the centroid has formed.
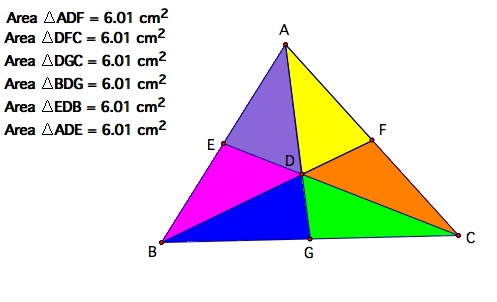
From our calculations in gsp the six triangles do have the same areas and so we can assume that triangle ADB, BDC and ADC would also have equal areas since they are formed by adding two of the smaller triangles together. Here is a gsp file so that you can move the triangle around and see that the areas are always equal.
Now we need to prove why this is so!


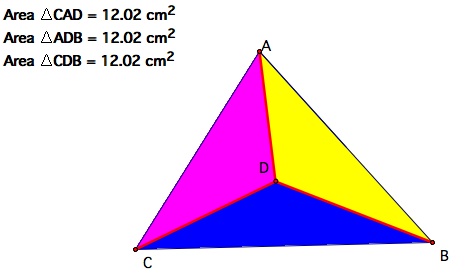
Here is a gsp file so you can move the triangle around yourself and see how the areas are equal. (this construction is on the third page)
To explore another trisection of triangles area click HERE!